¿Qué novedades tiene MetaTrader 5?
Historial de actualizaciones de las plataformas desktop, móvil y web
Terminal web
- Agregada la visualización de las fechas de inicio y finalización de la solicitud a las especificaciones de la herramienta:
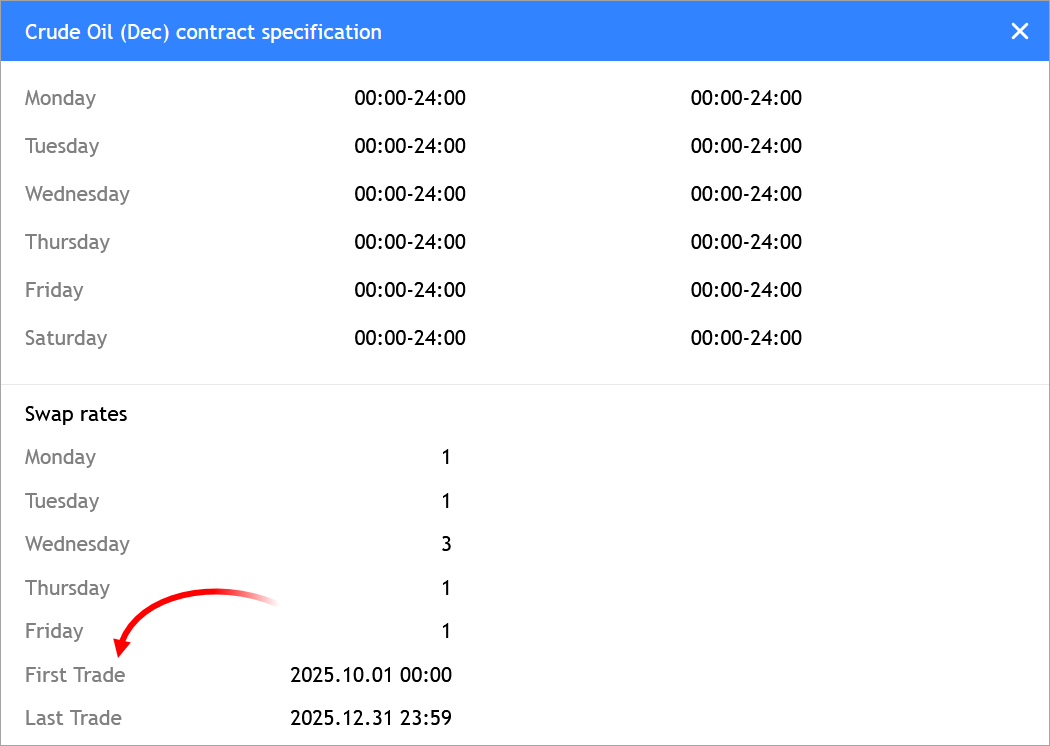
- Corregida la indexación del retraso de los precios en el apartado «Cotizaciones». En la vista de datos ampliada en dispositivos móviles, a veces no se mostraba el icono correspondiente.

- Corregida la visualización del menú para cambiar los marcos temporales. El problema sucedía en modo horizontal en los dispositivos móviles.
- Corregida la visualización de los tipos de cuentas disponibles en la ventana de apertura de cuentas demo.
- Corregida la localización de la ventana de conexión de la cuenta comercial. Algunos artículos podían mostrarse solo en inglés.
Terminal
- Añadida la comprobación de la longitud de la contraseña al conectarse a la cuenta por primera vez después de su migración desde MetaTrader 4. Ahora el sistema comprueba correctamente la complejidad de la nueva contraseña.
- Corregida la representación de la columna ID (ID en el sistema externo) en la lista de posiciones abiertas. Ahora solo se mostrará si al menos una de las operaciones de la lista tiene el identificador correspondiente.
MQL5
- Corregido el error presente en la generación de constructores implícitos y operadores de copiado para estructuras y clases. En algunos casos, podía provocar la finalización crítica de un programa MQL.
Terminal
- Añadido el soporte para programas MQL5 de tipo "Servicio" en la biblioteca de códigos.
A diferencia de los asesores expertos, los indicadores y los scripts, los servicios no están vinculados a un gráfico específico. Funcionan en segundo plano y se inician automáticamente al iniciarse el terminal. Con ellos, podrá implementar sus propias fuentes de datos de precios para la plataforma, así como realizar muchas tareas auxiliares.
Ahora existe una categoría aparte para estos programas. Los desarrolladores pueden compartir su código en CodeBase:
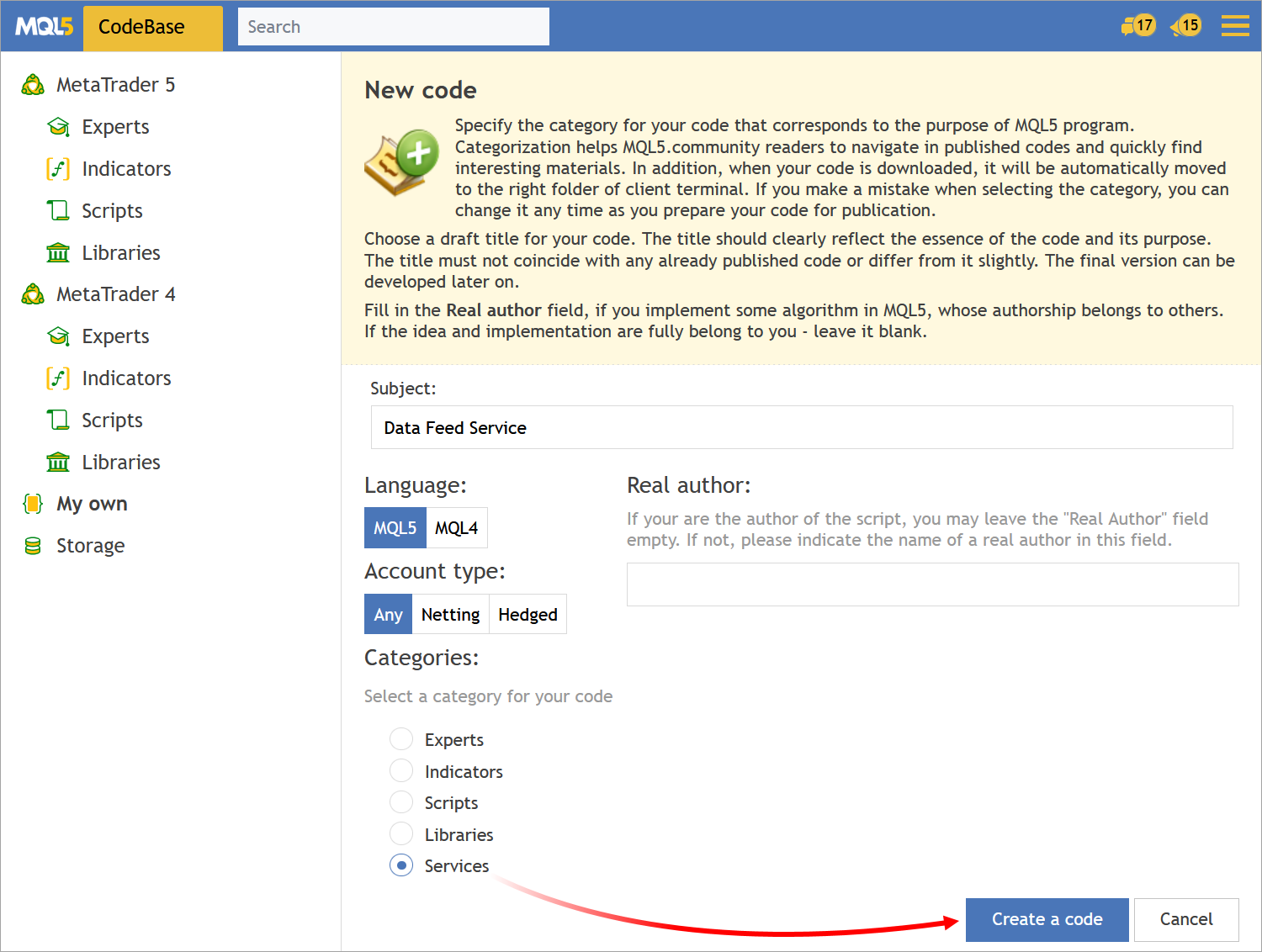
Los usuarios pueden descargarlos fácilmente directamente desde la plataforma o el MetaEditor. Cuando se descarga, el programa se coloca en la carpeta correspondiente y se compila automáticamente, por lo que puede ejecutarse de forma inmediata.
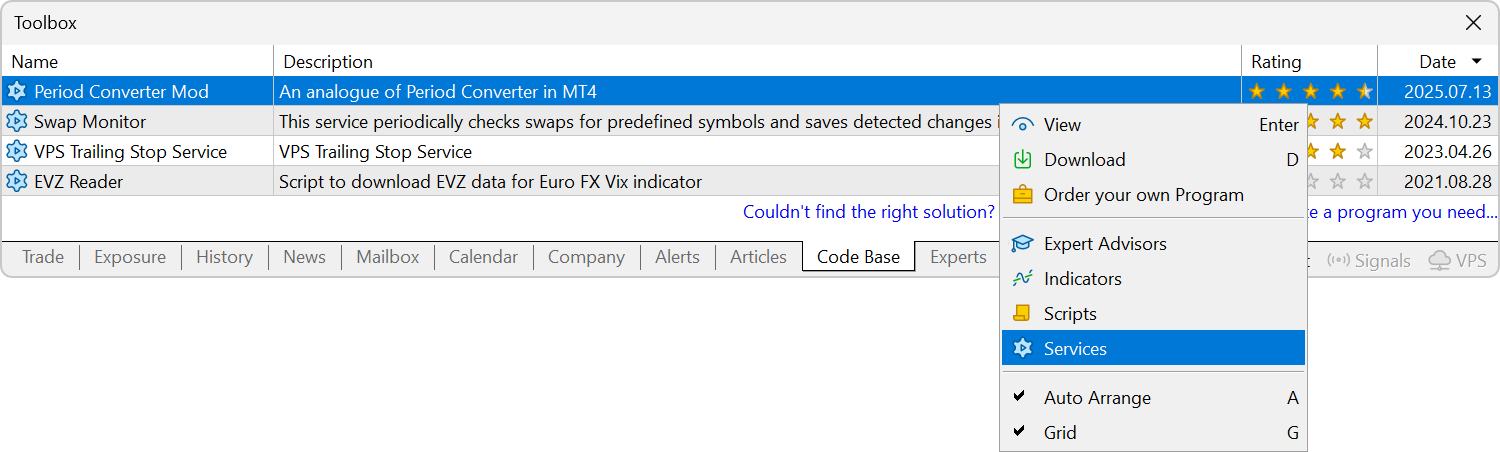
- Corregido el error que provocaba que los archivos de gráficos eliminados (cerrados) se movieran a un directorio incorrecto. Debido a ello, los usuarios no podían restaurar dichos gráficos a través del menú "Archivo / Abrir remoto".
MQL5
- Añadido el soporte para la nueva sintaxis de los parámetros de entrada. Ahora podrá establecer explícitamente un nombre visible para ellos, que se mostrará en las propiedades del programa en ejecución. Antes, se utilizaban comentarios para este fin.
En lugar de una sintaxis anticuada:input int InpVar; /*visible name*/ // some comment
Debe usarse:
input(name="visible name") int InpVar; // some comment
El nombre mostrado de la variable se especifica en el parámetro name. Solo se admite como valor una cadena literal.
Si se utiliza la nueva sintaxis de entrada, se ignorarán todos los comentarios posteriores a la declaración de la variable. La sintaxis anteriormente usada es compatible y no está marcada como obsoleta. Puede seguir utilizándola, el compilador no emitirá advertencias. - Corregido el error que podía provocar que el compilador imprimiera incorrectamente el mensaje «function must have a body».
MetaEditor
- Corregidas las sugerencias mostradas al pasar el cursor sobre el valor de la expresión observada en el depurador.
Tester
- Corregido el error de comprobación de los indicadores. Es posible que el proceso no se inicie si el nombre del indicador coincide con el nombre de la plantilla del gráfico.
Terminal web
- Añadida la traducción de la interfaz de usuario al rumano y al hebreo, mejoradas las traducciones de la ventana de conexión de cuentas.
- Corregida la visualización del menú de objetos en la versión móvil.
- Corregida la visualización fija del volumen mínimo y del paso de volumen en la especificación del contrato.
Terminal
- Corregida la visualización de los ajustes de margen en las especificaciones del instrumento comercial. Antes, al utilizarse el apalancamiento flotante (por ejemplo, según el volumen de las posiciones en la cuenta), en algunos casos la configuración del margen en las especificaciones del contrato se mostraba incorrectamente.
- Corregida la clasificación de las órdenes en la pila, si el símbolo permite comerciar con precios negativos. Las solicitudes con precios positivos, negativos y cero ahora se muestran correctamente y en el orden correcto.
- Añadido al manual del terminal el apartado Cómo el simulador descarga los datos históricos En él hemos reunido la información básica necesaria para comprender el trabajo del simulador de estrategias con la historia comercial. El simulador carga siempre un "búfer histórico previo al arranque" para garantizar la estabilidad de los cálculos:
- D1 y siguientes desde principios del año anterior. Esto ofrece una reserva de al menos 1 año de historia. Por ejemplo, si la fecha de inicio de la prueba es el 01.03.2023, el simulador descargará los datos del terminal histórico a partir del 01.01.2022. Es decir, 14 meses antes de la fecha de inicio de las pruebas.
- W1 - 100 barras semanales (~2 años).
- MN1 - 100 barras mensuales (~8 años).
Si existen menos datos, el simulador desplazará la fecha de inicio real a la fecha disponible más próxima en la que se cumplan las condiciones.
Debido a estos requisitos, a veces sucede que las pruebas no empiezan en la fecha especificada, sino en una fecha posterior. Y esto se ve acompañado de un mensaje en el diario del simulador:
start time changed to 2024.03.15 00:00 to provide data at beginning
MQL5
- Añadido 5 nuevos métodos a OpenBLAS: la nueva sección Matrix Balance, que amplía las posibilidades de trabajar con matrices cuadradas. El nuevo conjunto de funciones ofrece:
- Equilibrado de matrices para mejorar la precisión de los cálculos de valores propios.
- Recuperación de los vectores propios tras las transformaciones pertinentes.
- Reducción a la forma de Hessenberg y la descomposición de Schur, incluida la generación de matrices ortogonales.
Con estas herramientas, los desarrolladores conseguirán un ciclo de transformación completo: desde el preentrenamiento de la matriz hasta el cálculo preciso y estable de su espectro.
Para ello, se utilizan algoritmos LAPACK de eficacia probada (GEBAL, GEBAK, GEHRD, ORGHR, HSEQR) que garantizan un alto rendimiento y fiabilidad:
- MatrixBalance equilibra las matrices cuadradas (reales o complejas) usando permutaciones y/o escalado de filas y columnas. Reduce la norma 1, mejorando la precisión del cálculo posterior de los valores/vectores propios (usando como base la función LAPACK GEBAL).
- EigenVectorsBackward — forma vectores propios (derechos o izquierdos) de la matriz original después de equilibrar, ejecuta la transformación inversa (basada en GEBAK).
- ReduceToHessenbergBalanced — convierte la matriz equilibrada a la forma de Hessenberg triangular superior usando una transformación ortogonal (GEHRD).
- ReflectHessenbergBalancedToQ — genera una matriz ortogonal Q, que es el producto de matrices reflexivas formadas por reducción a la forma de Hessenberg (ORGHR).
- EigenHessenbergBalancedSchurQ — realiza la descomposición de Schur: calcula los valores propios de la matriz de Hessenberg, así como las matrices T (forma de Schur triangular superior) y Z (matriz vectorial), y de ser necesario, actualiza Q (HSEQR).
- Añadidos dos nuevos métodos a la sección Eigen Values.
Ambas funciones permiten obtener eficientemente los vectores propios
tras la descomposición de Shur y complementan el conjunto completo de
herramientas de álgebra lineal en MQL5:
- EigenVectorsTriangularZ — calcula los vectores propios de una matriz real cuasi-triangular superior o compleja triangular superior (forma de Schur). Utiliza la descomposición A = Q · T · Qᴴ (TREVC). Se caracteriza por su gran precisión.
- EigenVectorsTriangularZBlocked — variante en bloque del cálculo de vectores propios (TREVC3). Funciona más rápido que EigenVectorsTriangularZ, pero puede resultar menos precisa.
- Introducido un cambio importante en la herencia: la regla de method hiding.
Antes, si una clase o estructura derivada definía un método con el mismo nombre que en la clase básica, se producía la sobrecarga: todas las variantes de los métodos (tanto del ancestro como del descendiente) estaban disponibles en el descendiente. Ahora, los métodos con el mismo nombre en el descendiente ocultan los métodos del ancestro (method hiding).
Si necesita llamar a un método ancestro oculto, deberá especificar explícitamente el ámbito al llamarlo:class Base { public: void Print(int x) { ::Print("Base int: ", x); } void Print(double y){ ::Print("Base double: ", y); } }; class Derived : public Base { public: void Print(string s){ ::Print("Derived string: ", s); } }; void OnStart() { Derived d; d.Print("text"); // call of Derived::Print(string) d.Print(10); // ATTENTION! Calling Derived::Print(string) since Base::Print is hidden (inaccessible) d.Base::Print(10); // explicit call to hidden parent method }
Durante algún tiempo, el compilador MQL5 generará una advertencia si un método ancestro oculto es más adecuado según los parámetros de llamada que un método descendiente disponible. El ejemplo para el código anterior es d.Print(10):call resolves to 'void Derived::Print(string)' instead of 'void Base::Print(int)' due to new rules of method hiding
see declaration of function 'Derived::Print'
see declaration of function 'Base::Print'
implicit conversion from 'number' to 'string'
- Añadido el operador using para recuperar sobrecargas de métodos ancestros.
Para gestionar el nuevo comportamiento, en MQL5 ha aparecido el operador using. Este permite "atraer" al ámbito de una clase o estructura todas las sobrecargas de métodos del tipo básico:
class Base { protected: void Print(int x) { ::Print("Base int: ", x); } void Print(double y){ ::Print("Base double: ", y); } }; class Derived : public Base { public: void Print(string s){ ::Print("Derived string: ", s); } using Base::Print; // return Print overloads from Base }; void OnStart() { Derived d; d.Print("text"); // Derived::Print(string) d.Print(42); // Base::Print(int) d.Print(3.14); // Base::Print(double) }
Si eliminamos using Base::Print;, las llamadas d.Print(42) y d.Print(3.14) no estarán disponibles, solo quedará el método Derived::Print(string)
Además, en el ejemplo anterior, podemos ver que los métodos protegidos del ancestro ahora están disponibles en el descendiente (protected ha cambiado a public)
De este modo, los desarrolladores tienen ahora un control más flexible y predecible sobre las jerarquías de las clases y pueden determinar exactamente qué sobrecargas de los métodos del ancestro deben permanecer disponibles en el descendiente.
MetaEditor
- Acelerados los cálculos hash SHA-1 para operaciones Git al trabajar con Algo Forge. El resultado es un aumento de la productividad de más de un 40% en las operaciones masivas.
- Corregida la lógica de comprobación de las modificaciones de archivos para operaciones Git. Si solo hemos cambiado la hora de modificación pero el contenido sigue siendo el mismo, el archivo ya no se considerará modificado. Esto eliminará las falsas detecciones y evitará conflictos con el repositorio remoto.
Algo Forge
- almacenamiento seguro de la historia de versiones y la gestión de ramas
- experimentación rápida y fusión segura de los cambios,
- repositorios propios o bifurcaciones del proyecto de otra persona con un solhttps://www.mql5.com/go?link=https://forge.mql5.io/help/en/guideo clic,
- trabajo en equipo transparente en el que se registrará la contribución de todos,
- catálogo de proyectos abiertos y la oportunidad de aprender de los demás.
Clonación de proyectos ajenos
En forge.mql5.io, vaya al proyecto que desea clonar y ejecute el comando Fork. Rellene el nombre de la bifurcación que está creando con su correspondiente descripción, y guarde luego los cambios:
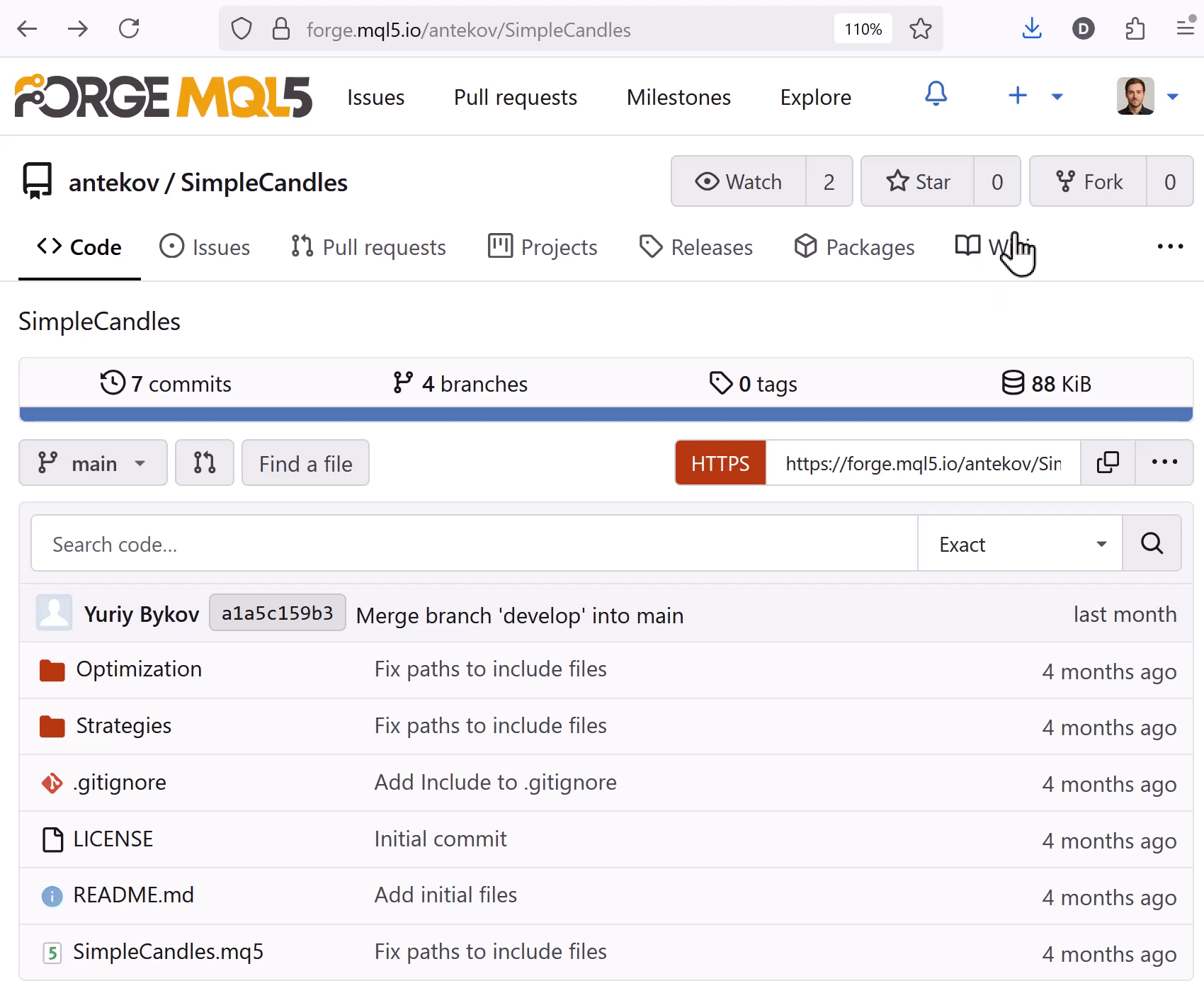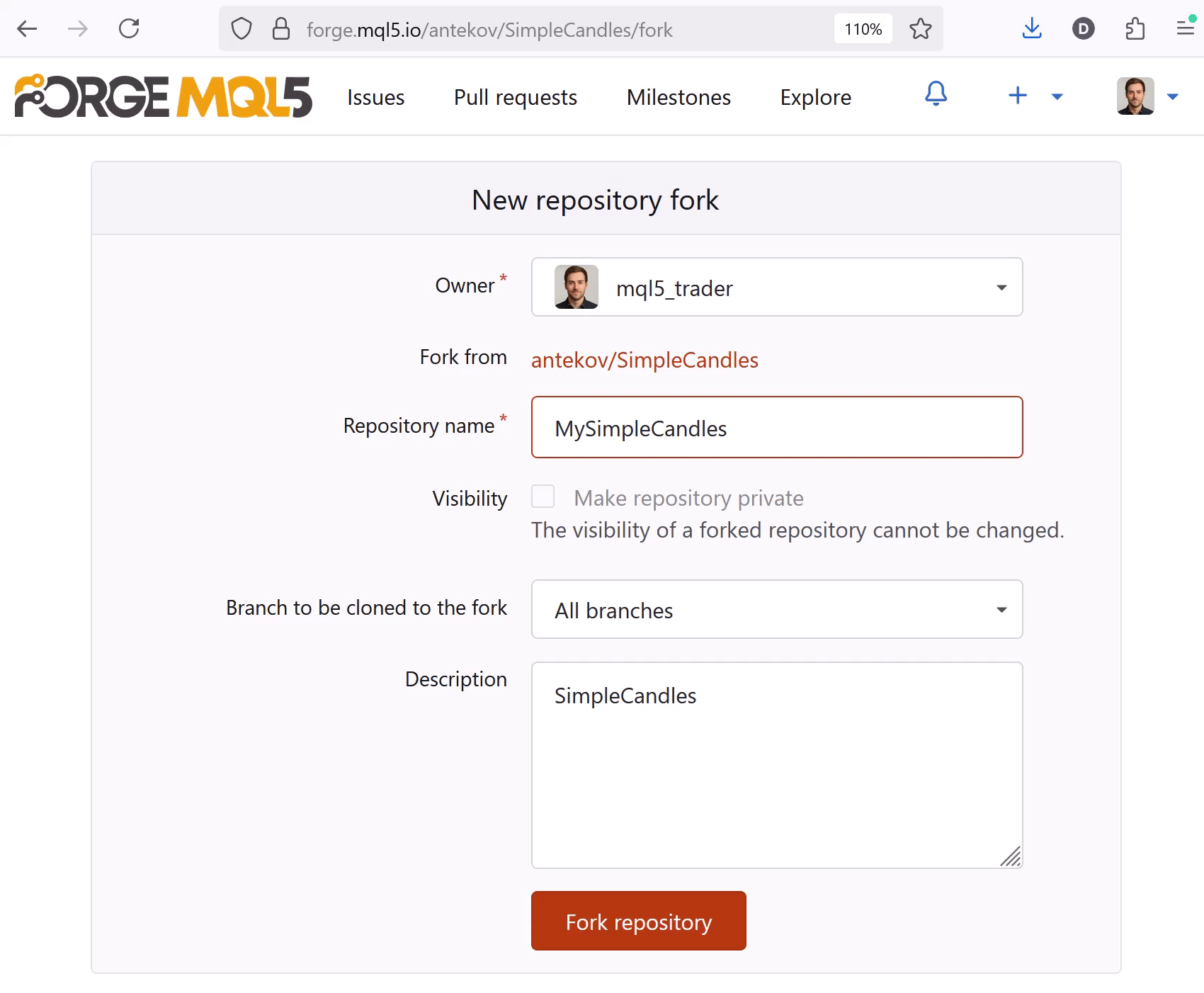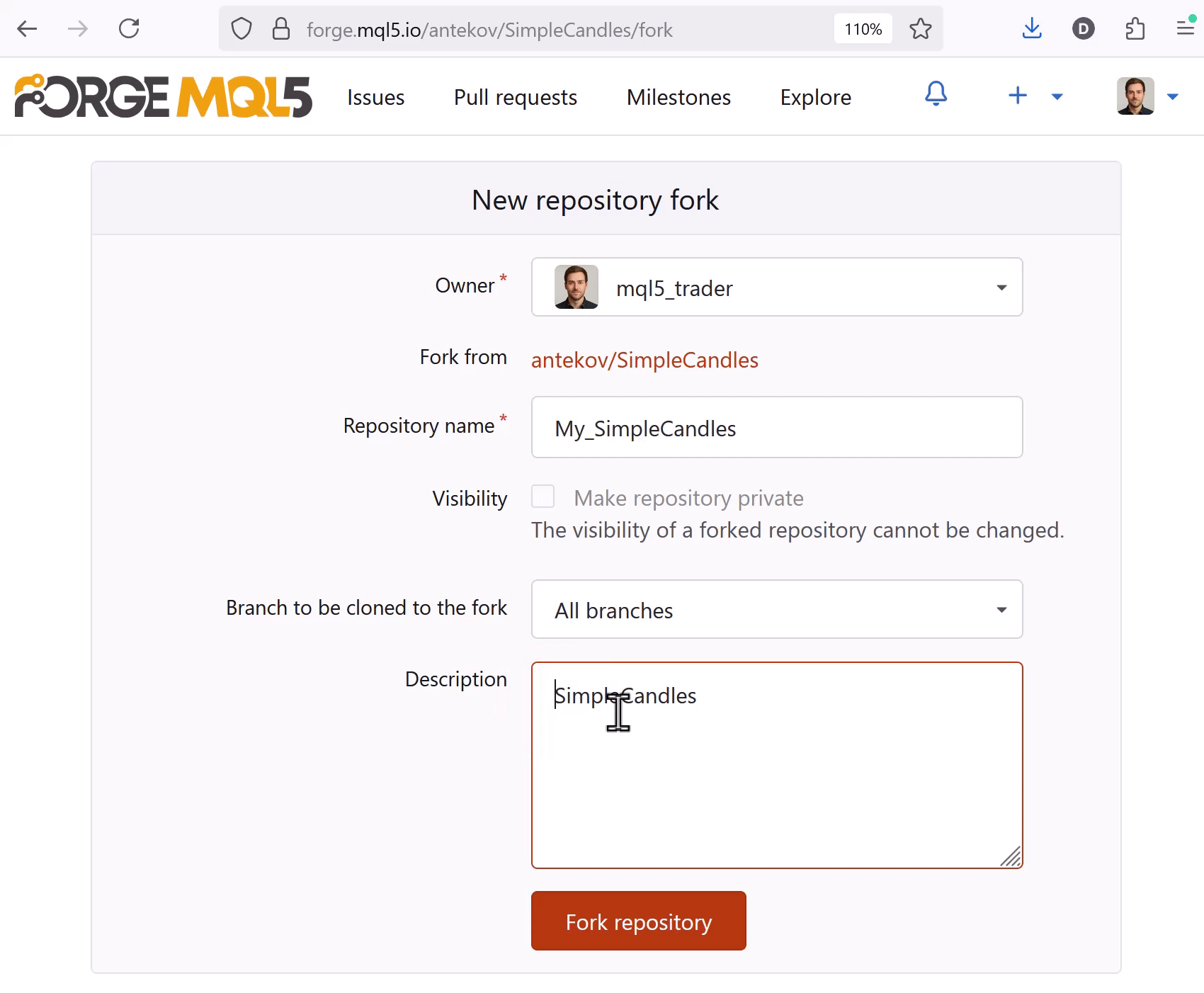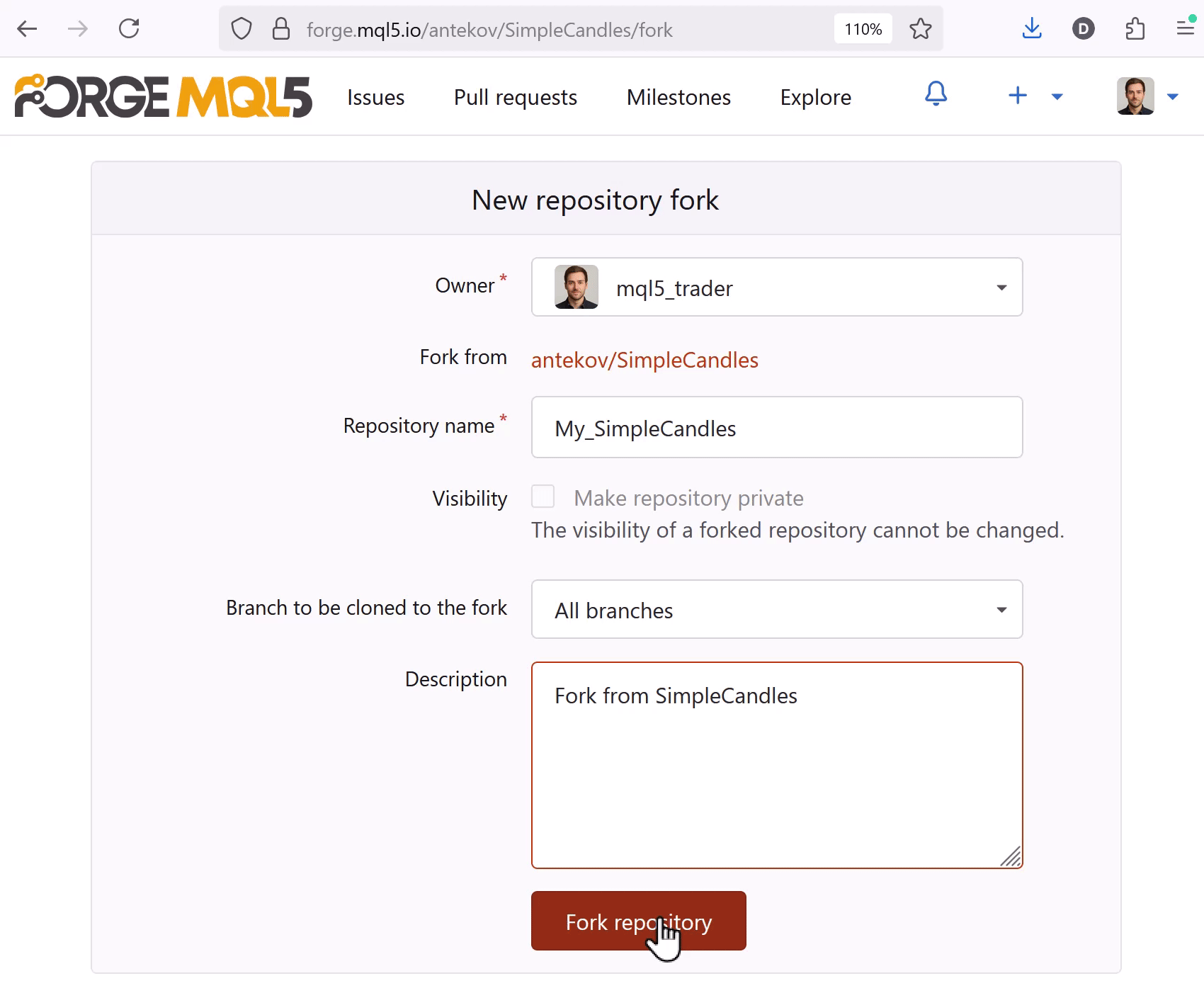
A continuación, vaya a MetaEditor con la misma cuenta MQL y ejecute el comando (Refresh) en el Navegador. El proyecto clonado aparecerá en la carpeta Shared projects. Ahora cárguelo desde el portal Algo Forge con el comando Git Clone. Descargará no solo todos los archivos del proyecto, sino también toda la historia de confirmaciones y todas las ramas de ese proyecto. Es decir, podrá seguir trabajando en la bifurcación con toda la historia del proyecto clonado.

Web Terminal
- Corregida la visualización de la hora de la sesión de trabajo y de cotización en las especificaciones del símbolo
- Corregida la visualización de la configuración de márgenes en las especificaciones del símbolo
- Modificada la visualización de las sesiones de los instrumentos comerciales en las especificaciones del símbolo
- Añadido soporte para cuentas comerciales de tipo Contest, estas cuentas se muestran en color azul, las Demo, en verde.
- Corregida la precisión de los cálculos de márgenes con apalancamiento flotante en algunos casos.
- Corregido el siguiente error al abrir una cuenta nueva: en algunos casos, el botón "Next" para pasar al siguiente paso no funcionaba.
- Corregido el error que impedía colocar una orden límite entre los precios de compra y venta en el modo de ejecución bursátil.
- Corregido el error de visualización del precio de ejecución de una orden. Tras el envío de la orden, en la ventana se mostrará el resultado de su ejecución: la ejecución con éxito de la operación comercial o el rechazo con la descripción del motivo donde se explica porqué no ha sido ejecutada. En algunos casos, el precio de ejecución aparecía como "0".
- Corregido el error que impedía mostrar el botón de cierre rápido de posiciones.

- Corregida la visualización de las divisas de las cuentas comerciales en la ventana de selección de la lista de cuentas.
Terminal
- Añadida la posibilidad de aplicar automáticamente un tema de interfaz claro u oscuro en función de la configuración de Windows. Para ello, active la nueva opción "Ver / Esquemas de color / Sistema". Cada vez que se inicie, la plataforma comprobará qué interfaz está usando en el sistema y se adaptará en consecuencia.
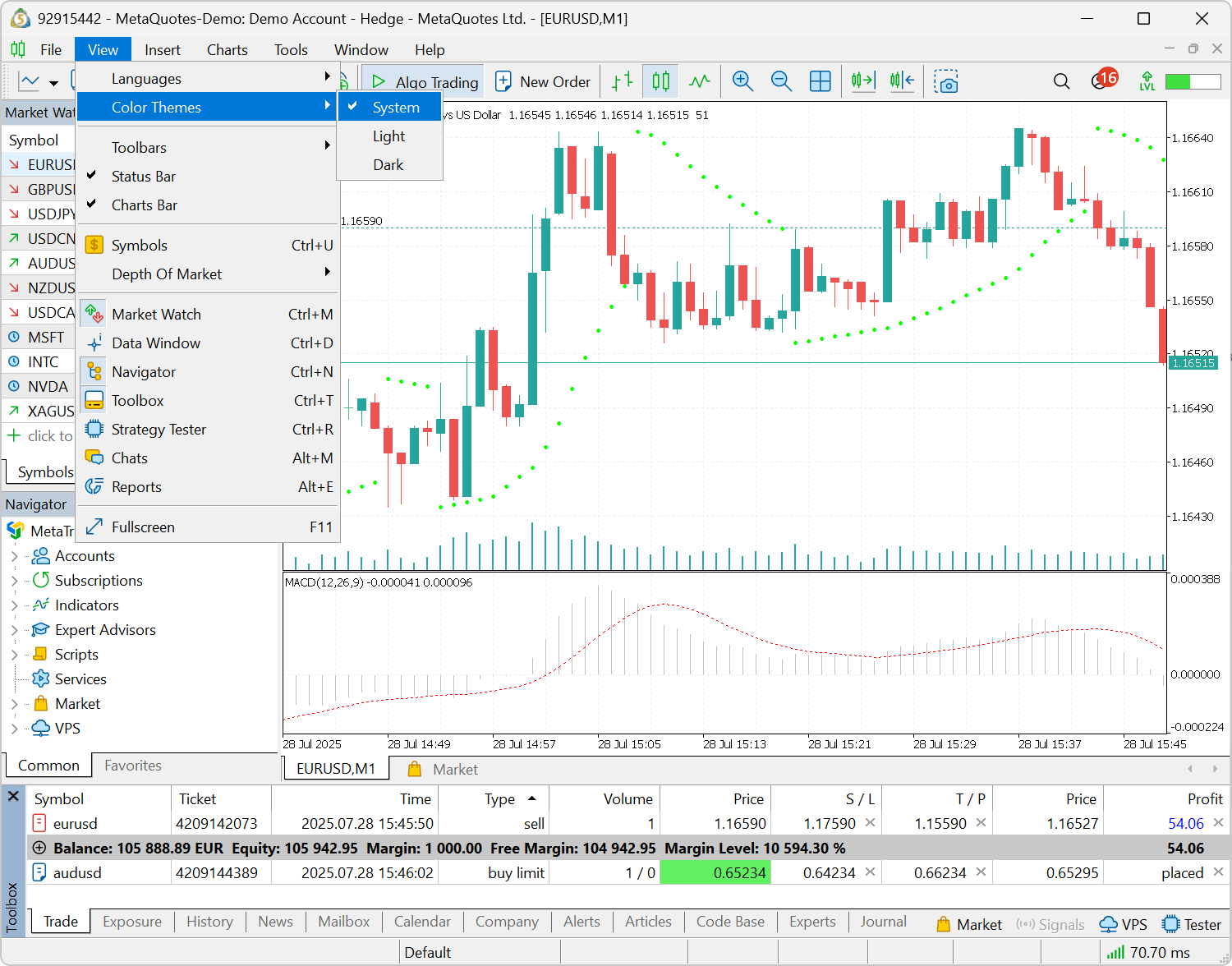
- Corregida la visualización de los paneles de instrumentos separadas de la ventana principal.
- Corregido el cálculo del valor de liquidación del portafolio en la sección «Activos». Para algunos instrumentos podían no registrarse posiciones.
- Corregida la visualización de los precios negativos en la profundidad de mercado. Ahora estarán ordenados correctamente.
- Corregida la importación de la historia de precios en los instrumentos comerciales personalizados. En el caso de los instrumentos situados en la carpeta raíz, es posible que los comandos correspondientes no estuvieran disponibles.
- Actualizadas las traducciones de la interfaz de usuario.
MQL5
- Añadidos nuevos métodos OpenBLAS:
Conversión matricial
- ReduceToHessenberg — convierte una matriz general real o compleja A de tamaño n por n a la forma superior de Hessenberg B utilizando una transformación ortogonal de similitud: Q**T * A * Q = H. Función LAPACK de GEHRD.
- ReflecHessenbergToQ — genera una matriz ortogonal Q, que se define como el producto de n-1 reflectores elementales de orden n devueltos por la función ReduceToHessenberg: Q = H(1) H(2) . . . H(n-1). Función LAPACK de ORGHR.
Cálculo de valores y vectores propios
- EigenHessenbergSchurQ — calcula los valores propios de la matriz de Hessenberg H y las matrices T y Z a partir de la descomposición de Schur: H = Z T Z**T. Aquí T es la matriz cuasi triangular superior (forma de Schur), mientras que Z es la matriz ortogonal de vectores de Schur. Función LAPACK de HSEQR.
Resolución de sistemas de ecuaciones lineales
- SylvesterEquationTriangular — resuelve la ecuación de Sylvester para matrices reales cuasi triangulares o complejas triangulares: op(A)*X + X*op(B) = scale*C o op(A)*X - X*op(B) = scale*C, donde op(A) = A o A**T o A**H, а A y B son triangulares superiores. Función LAPACK TRSYL.
- SylvesterEquationTriangularBlocked — resuelve la ecuación de Sylvester para matrices reales cuasi triangulares o complejas triangulares: op(A)*X + X*op(B) = scale*C o op(A)*X - X*op(B) = scale*C, donde op(A) = A, A**T o A**H, а A y B son matrices triangulares superiores. Función LAPACK de TRSYL3. Esta es la versión en bloque (BLAS nivel 3) de TRSYL. Es hasta 5 veces más rápida, pero menos precisa.
Cálculos factorizados
- SylvesterEquationSchur — resuelve la ecuación de Sylvester para matrices reales cuasi triangulares o complejas triangulares: A*X + X*B = C, donde A y B son matrices triangulares superiores. A tiene un tamaño de m por m, mientras que B tiene un tamaño de n por n; el lado derecho de C y la solución de X tienen un tamaño de m por n. Función LAPACK TRSYL.
- SylvesterEquationSchurBlocked — resuelve la ecuación de Sylvester para matrices reales cuasi triangulares o complejas triangulares: A*X + X*B = C, donde A y B son matrices triangulares superiores. A tiene un tamaño de m por m, mientras que B tiene un tamaño de n por n; el lado derecho de C y la solución de X tienen un tamaño de m por n. Función LAPACK de TRSYL3. Esta es la versión en bloque (BLAS nivel 3) de TRSYL. Es hasta 5 veces más rápida, pero menos precisa.
Cálculo de normas matriciales para diferentes estructuras
- MatrixNorm — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz rectangular de forma general. Función LAPACK de LANGE.
- MatrixNormGeTrid — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz tridiagonal general. Función LAPACK de LANGT.
- MatrixNormHessenberg — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de la matriz superior de Hessenberg. Función LAPACK de LANHS.
- MatrixNormSy — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz real simétrica o hermitiana compleja. Funciones LAPACK de LANSY y LANHE.
- MatrixNormComplexSy — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz simétrica compleja (no hermitiana). Función LAPACK de LANSY.
- MatrixNormSyTrid — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz tridiagonal real simétrica o hermitiana compleja. Funciones LAPACK de LANST y LANHT.
- MatrixNormTriangular — devuelve el valor de la norma 1, la norma infinita, la norma de Frobenius o el mayor valor absoluto de cualquier elemento de una matriz trapezoidal de tamaño m por n o de una matriz triangular. Función LAPACK de LANTR.
Análisis de las propiedades estructurales de las matrices
- IsSymmetric — comprueba si una matriz cuadrada es simétrica.
- IsHermitian — comprueba si una matriz compleja cuadrada es hermitiana.
- IsUpperTriangular — comprueba si una matriz cuadrada es triangular superior.
- IsLowerTriangular — comprueba si una matriz cuadrada es triangular inferior.
- IsTrapezoidal — comprueba si una matriz rectangular (no cuadrada) de tamaño m por n es trapezoidal superior o inferior.
- IsUpperHessenberg — comprueba si una matriz cuadrada es una matriz de Hessenberg superior.
- IsLowerHessenberg — comprueba si una matriz cuadrada es una matriz de Hessenberg inferior.
- IsTridiagonal — comprueba si una matriz cuadrada es tridiagonal.
- IsUpperBidiagonal — comprueba si una matriz cuadrada es bidiagonal superior.
- IsLowerBidiagonal — comprueba si una matriz cuadrada es bidiagonal inferior.
- IsDiagonal — comprueba si una matriz cuadrada es diagonal.
- IsScalar — comprueba si una matriz cuadrada es escalar.
- Añadido el método Conjugate para matrices y vectores complejos. Cambia el signo de la parte imaginaria de un número complejo y retorna la matriz o vector modificados.
- Reforzadas las normas para ocultar métodos. Cuando una clase derivada tiene un método con el mismo nombre que la clase básica, ahora se llamará por defecto a la versión de la clase derivada. Para hacer referencia al método básico, ahora se requerirá un calificador:
struct A { int y; string func(double x) { return(__FUNCSIG__); } }; struct B : public A { string func(int x) // the method hides A::func { return(__FUNCSIG__); } }; void OnStart(void) { B b; b.func(M_PI); // according to new rules, it is a call to B::func b.A::func(M_PI); // call the hidden method A::func }
Esto simplificará la lectura del código y eliminará la ambigüedad que antes solo iba acompañada de una advertencia del compilador.
Antes se daba una advertencia al compilar:deprecated behavior, hidden method calling will be disabled in a future MQL compiler versionEste cambio ya ha entrado en vigor.
En algunos builds, en el diario se registrará una advertencia si existe un método oculto más apropiado según los parámetros.
call resolves to 'string B::func(int)' instead of 'string A::func(double)' due to new rules of method hiding
see declaration of function 'B::func'
see declaration of function 'A::func'
truncation of constant value from 'double(3.141592653589793)' to 'int(3)' - Prohibidos los nombres duplicados en el mismo ámbito. Por ejemplo, antes se podía declarar un parámetro de entrada y una función homónima en el mismo archivo. Tal duplicación resultará ahora inaceptable:
input int somename=42; int somename(int x) { return(42); }
- Añadida la comprobación estricta de los tipos de valores por defecto en las enumeraciones. Para las funciones-parámetro que admiten enum, ahora no solo se comprueba el valor, sino también que el tipo coincida exactamente:
int somename(ENUM_TIMEFRAMES TF=PERIOD_CURRENT); int somename(ENUM_TIMEFRAMES TF=0) // error, type mismatch for the default parameter value, despite having the same value { return(42); }
- Prohibidos los identificadores idénticos en enumeraciones diferentes. Ahora, un identificador de una enumeración no puede repetirse en otra enumeración del mismo ámbito:
enum A { Value }; enum B { Value // error, name 'Value' is already used in enumeration A }; void OnStart(void) { enum C { Value // OK, 'Value' is not used within the OnStart scope }; }
En ámbitos diferentes, sí se pueden utilizar los mismos nombres. - Activados requisitos estrictos para las funciones inicializadoras de plantillas. Al crear matrices/vectores a través de funciones inicializadoras se desactivan:
- El autotipado de funciones de plantilla
- Los valores por defecto de los parámetros.
Ahora se deben especificar explícitamente los parámetros de la plantilla y todos los argumentos:template<typename T> void Initializer(matrix<T>& mat,int method=0); matrix<double> A(10,10,Initializer,42); // error, Initializer must be explicitly typed matrix<double> A(10,10,Initializer<double>); // error, missing 'method' parameter (default values no longer supported) matrix<double> A(10,10,Initializer<double>,42); // OK
- Mejorada la compatibilidad con ONNX. Añadida conversión implícita del tipo de signo al transmitir matrices ulong en funciones, lo que facilita la integración de MQL5 con modelos ONNX.
OnnxSetInputShape( … , ulong_array );
OnnxSetOutputShape( … , ulong_array ); - Corregida la visualización de tipos en los avisos de conversión implícita de cadenas.
- Actualizado el paquete de integración con Python. Para instalar la actualización, ejecute el comando
pip install --upgrade MetaTrader5
MetaEditor
- Corregidos los comandos "Roll back to revision" utilizados para MQL5 Storage. La evaluación de los conflictos entre versiones que puedan surgir durante la reversión se realiza ahora antes de la operación. Si no es posible la reversión, la operación se cancelará.
- Actualizadas las traducciones de la interfaz de usuario.
Tester
- Corregido el funcionamiento de la función OrderCalcMargin para las cuentas del modelo bursátil de cálculos.
- Corregida la alternancia entre gráficos durante las pruebas visuales de los asesores expertos multidivisa.
Terminal web
- Corregida la verificación del correo electrónico al abrir cuentas demo y preliminares. En algunos casos, no aparecía el campo para introducir el código de confirmación.
- Corregida la conexión de la cuenta al trabajar en el navegador Huawei.
- Corregida la conexión a cuentas al utilizar contraseñas de un solo uso. En algunos casos, era posible que el campo de la contraseña de un solo uso no estuviera disponible al conectarse a la cuenta por primera vez.
Las últimas versiones de la aplicación móvil MetaTrader 5 para iOS
incluyen una serie de nuevas funciones para ayudar a los tráders a
seguir el pulso de los mercados financieros estén donde estén.
- Añadido un informe
que permite evaluar los resultados de las operaciones de una forma
visual y práctica. Le ayudará a optimizar su portafolio, a comprender
cómo reducir el riesgo y a mejorar la estabilidad de sus transacciones.
Para analizar su estrategia, entre en la sección de la historia y clique
en el icono de selección de periodo. A continuación, seleccione un
periodo y clique en "Crear informe comercial".
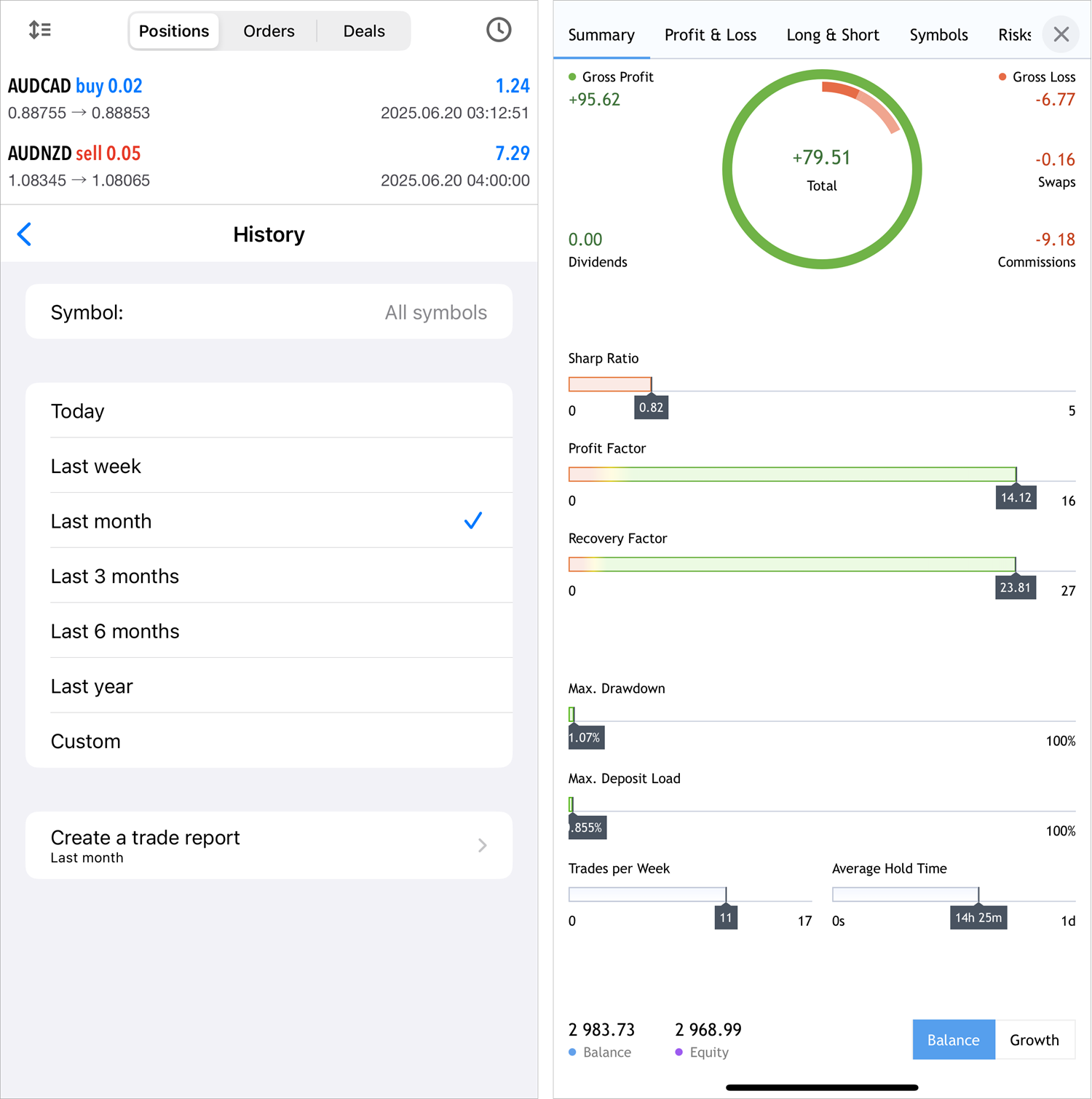
El informe está dividido en varias pestañas, cada una de las cuales contiene información añadida en su propia sección:
- Summary — información resumida sobre las transacciones realizadas durante todo el tiempo: datos de la cuenta, pérdidas y ganancias totales, importes depositados y retirados, balance, gráficos de crecimiento y dividendos y otros resultados de las transacciones.
- Profit/Loss — información sobre transacciones rentables y perdedoras. Se divide según el tipo de comercio (manual, algorítmico y copiado de transacciones); los resultados pueden analizarse según las transacciones o el dinero por meses y años.
- Long/Short — muestra la relación entre compras y ventas en dinámica y en intervalos de tiempo especificados, y también permite evaluar la rentabilidad en las direcciones Buy y Sell.
- Symbols — análisis de transacciones según los instrumentos financieros. Aquí verá en qué símbolos gana o pierde, con qué frecuencia comercia con ellos, los gráficos de transacciones y los volúmenes de dinero en ellos.
- Riesgos — indicadores básicos del riesgo de su estrategia: gráficos de reducción y carga de depósito, ratios de transacciones rentables y perdedoras.
- Añadidos los indicadores ZigZag y Market Profile, así como un nuevo tipo de gráfico: Heikin Ashi. Estas herramientas le ayudarán a comprender mejor el mercado y a identificar tendencias.
Para añadir nuevos indicadores, abra el menú del gráfico, haga clic en "Ventana principal" y selecciónelos de la lista: ZigZag se encuentra en los indicadores de tendencia, y Market Profile, en indicadores de volumen.
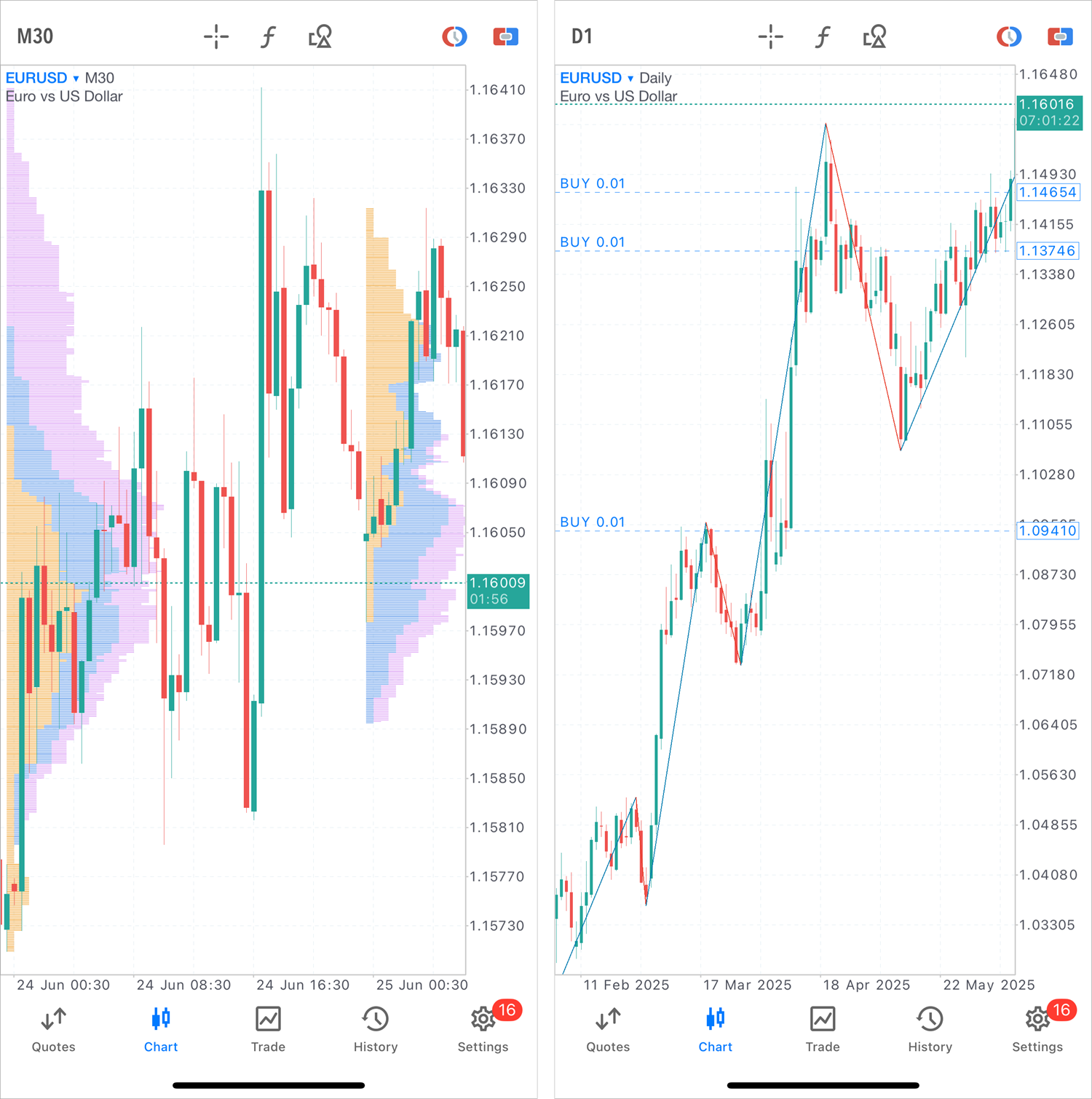
Para ver el gráfico Heikin Ashi, clique en el gráfico y vaya a la configuración.
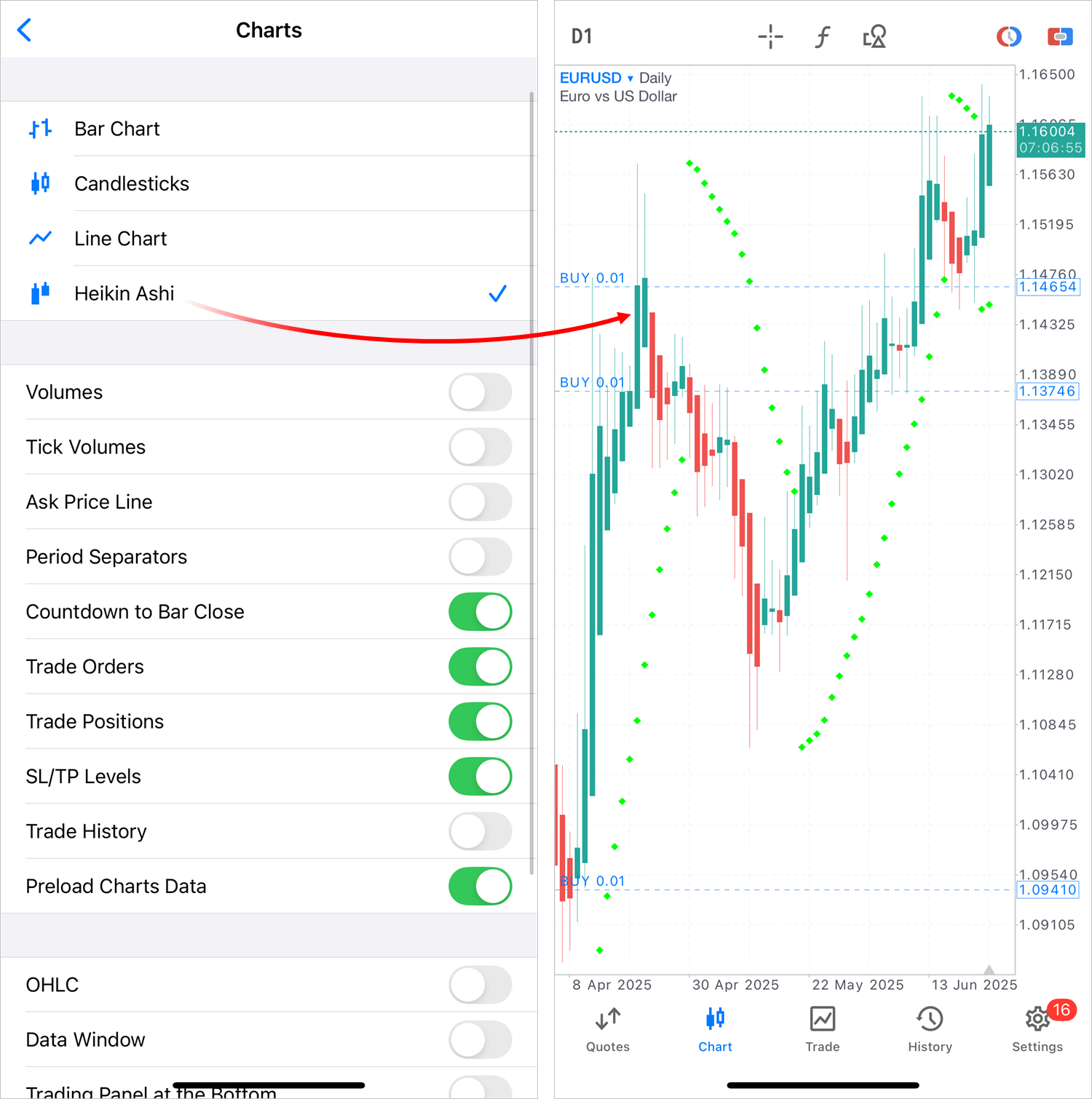
- Añadida la visualización de los datos de las transacciones en la ventana de datos.
Si pasa el cursor por encima de una barra durante la cual se hayan
ejecutado transacciones, la ventana de datos mostrará no solo los
precios y los valores de los indicadores, sino también los datos
generales sobre la transacción: dirección, entrada, volumen, precio y
resultado financiero.
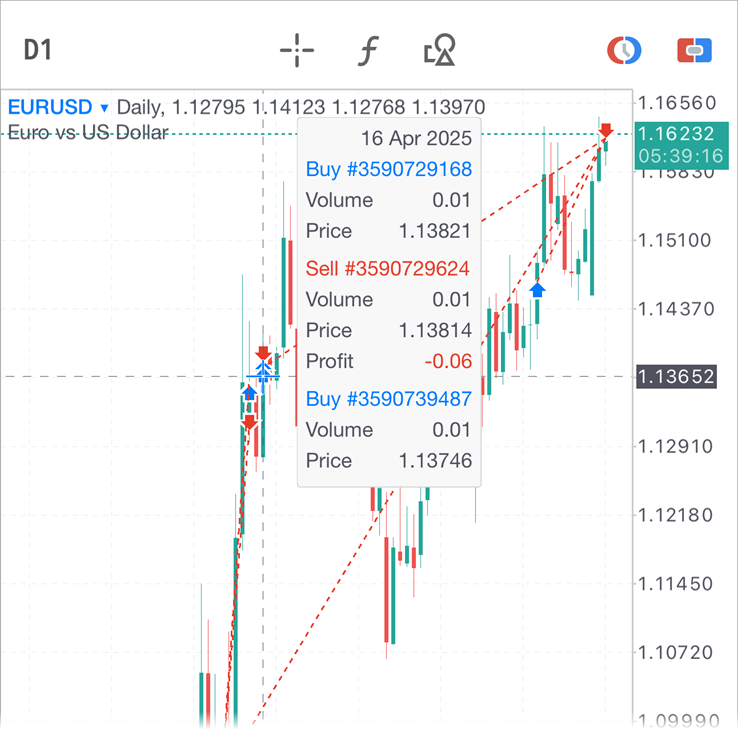
- Añadido un modo de llamada rápida de la ventana de datos en el gráfico. Ahora, una pulsación larga (más de un segundo) en el gráfico principal activará el modo de retícula y abrirá la ventana de datos. En cuanto suelte el dedo, el gráfico volverá al modo normal. Esto le permitirá ver rápidamente los valores exactos de las barras, los indicadores y las transacciones sin tener que cambiar al modo de retícula a través del panel superior.
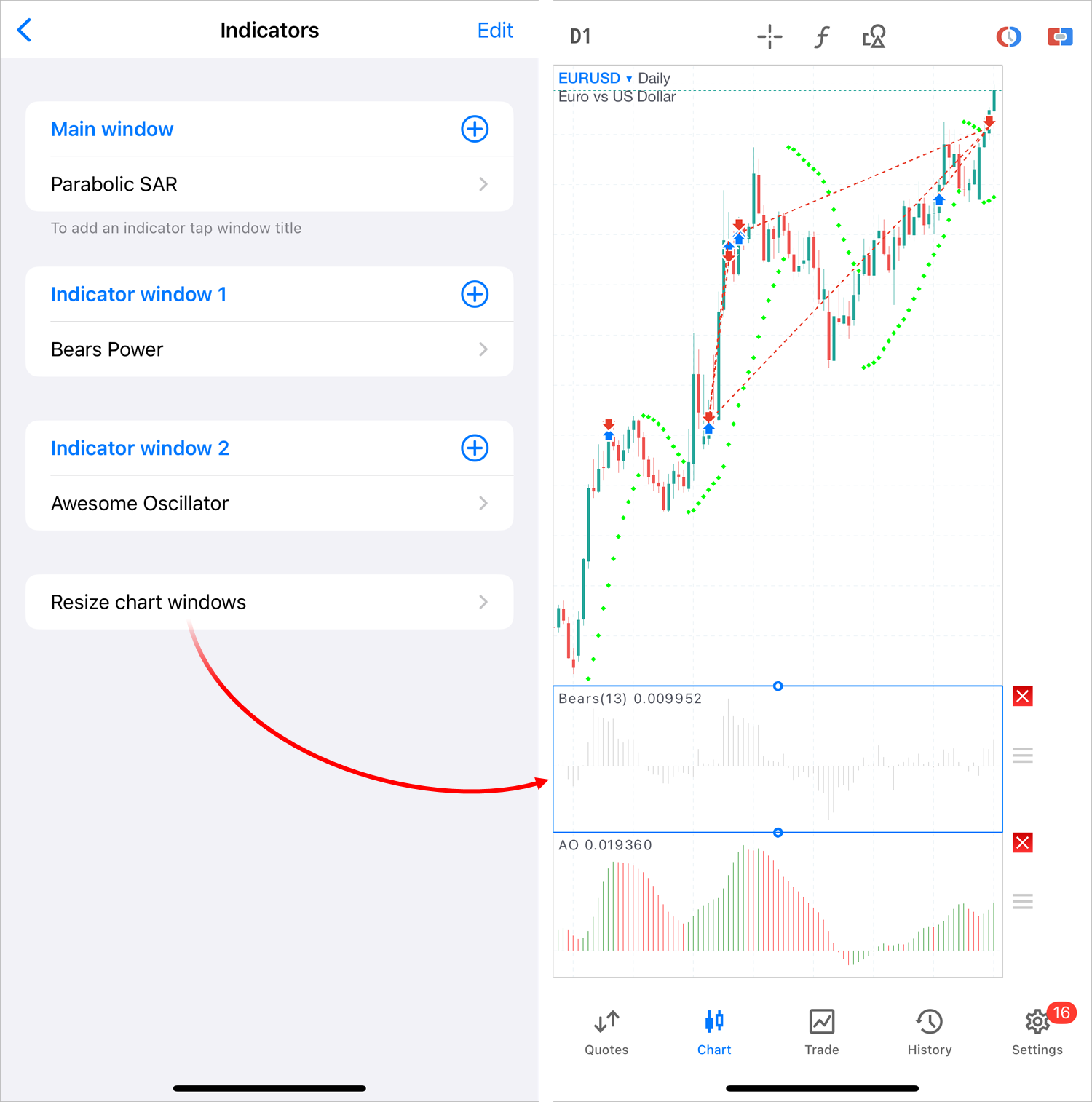
- Añadido un comando independiente para cambiar el tamaño y el
orden de las ventanas adicionales de los indicadores. La misma acción
puede realizarse pulsando prolongadamente la subventana del indicador en
el gráfico. También se ha mejorado el propio modo de edición de
subventanas: hemos añadido iconos adicionales para mayor claridad.
- Optimizada la visualización de la historia comercial en el gráfico. Ahora la aplicación puede mostrar miles de transacciones sin que el rendimiento disminuya significativamente.
Instale la última versión de la aplicación y amplíe sus posibilidades comerciales:
 |
|
Terminal
- Corregidos los errores de visualización de la interfaz gráfica al trabajar en Linux y macOS.
- Mejorado el mecanismo de actualización de la plataforma. Ahora la biblioteca estándar MQL5 no se reemplazará por completo cada vez, sino solo los archivos que realmente se hayan modificado.
- Añadido el restablecimiento del modo de visualización de pantalla completa al reiniciar la aplicación. Ahora, cada vez que inicie el programa, tendrá una interfaz completa.
MQL5
- Permitida la transmisión de arrays con conversión según el signo para las siguientes funciones:
- ArraySwap
- WebRequest
- CryptEncode
- CryptDecode
- StringToCharArray
- CharArrayToString
- StringToShortArray
- ShortArrayToString
- StructToCharArray
- CharArrayToStruct
- Corregida la obtención del estado de las teclas para los programas MQL en el gráfico activo usando la función TerminalInfoInteger.
- Corregido el funcionamiento de la función ArrayInitialize para arrays de enumeración.
MetaEditor
- Actualizados los modelos disponibles para AI Assistant. Ahora son compatibles todos los modelos GPT-4.1 y 04-mini.
- Activadas las comprobaciones precisas del estado de los archivos en el repositorio MQL5. Ahora se comprueba el hash de los archivos, lo cual elimina la visualización de indicadores falsos. Antes se podía usar un icono rojo para marcar archivos que en realidad no tenían cambios locales en comparación con la versión en el repositorio.
- Actualizadas las traducciones de la interfaz de usuario.
MetaEditor
- Hemos actualizado completamente el repositorio de código fuente MQL5 Storage. Ahora usa Git en lugar de Subversion como sistema de control de versiones. Se trata de un estándar para desarrolladores de todo el mundo que ofrece fiabilidad y flexibilidad en la gestión del código.
- Bifurcación y fusión flexibles: cree ramas independientes para nuevas funciones o experimentos y, a continuación, combine fácilmente estas en la versión principal del proyecto.
- Operaciones de repositorio más rápidas: a diferencia de Subversion, Git almacena todos los datos de manera local, lo cual hace que las operaciones (confirmaciones, cambio entre versiones, comparación de cambios) resulte mucho más rápidas.
- Trabajo sin conexión: ahora no necesita una conexión constante al servidor; podrá confirmar los cambios localmente y enviarlos al repositorio en línea cuando le convenga.
- Seguimiento avanzado de cambios: Git facilita la visualización de la historia de cambios, el seguimiento de quién ha realizado los mismos y cuándo, así como la vuelta a versiones anteriores sin complicaciones.
- Mejor fusión de cambios: el sistema avanzado de comparación y combinación de código permite minimizar los conflictos y gestionar fácilmente el desarrollo colaborativo.
Desarrollo conjunto a un nuevo nivel
Junto con la transición a Git, hemos abierto un nuevo portal para la gestión de proyectos en línea: MQL5 Algo Forge. No se trata solo de una lista con sus proyectos, es toda una red social para desarrolladores, una especie de GitHub para tráders algorítmicos. Suscríbase a autores interesantes, cree equipos y dirija cómodamente proyectos de colaboración.
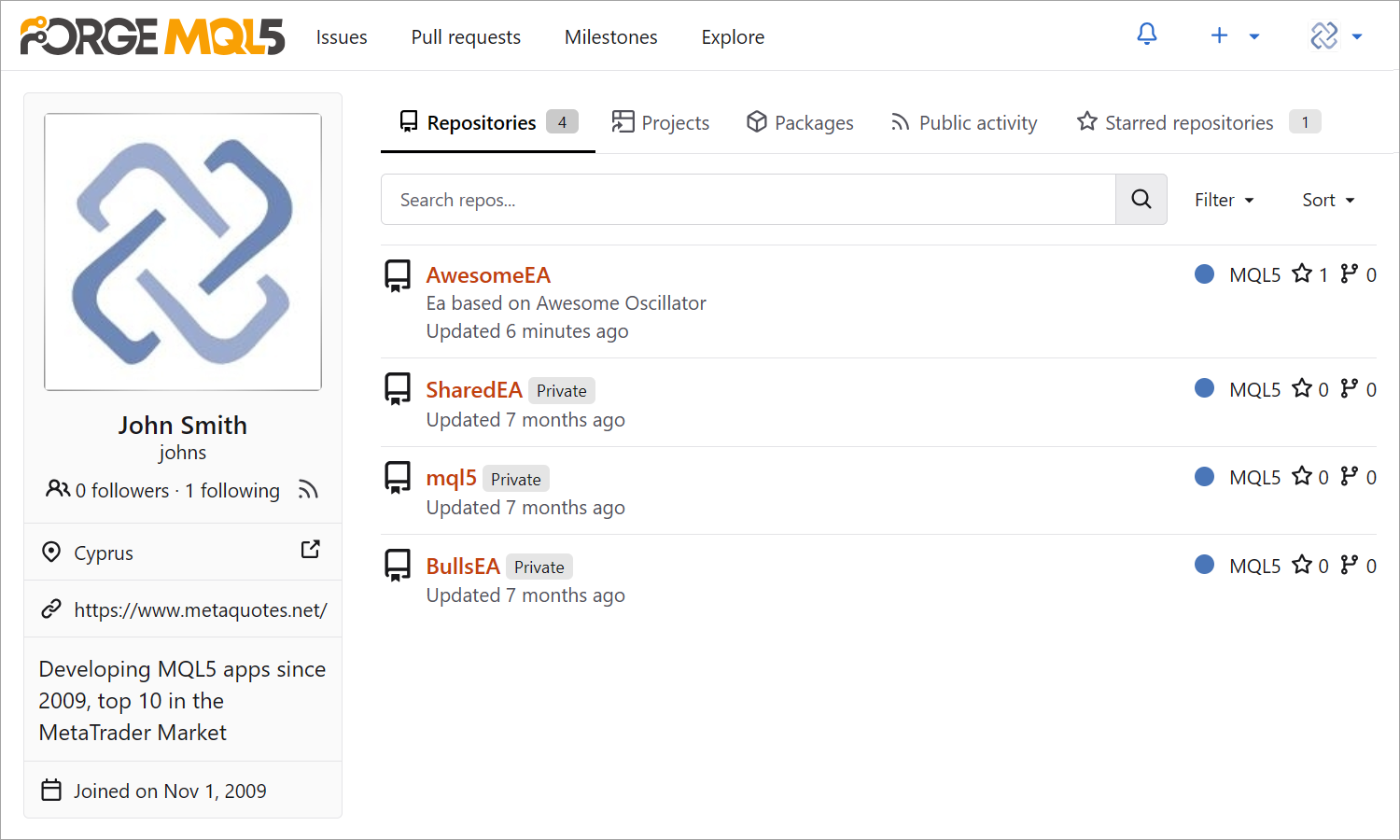
Vea los detalles del proyecto: estructura, archivos, commits, ramas, etc. Monitoree la contribución de cada integrante, cree documentación y comparta el proyecto en línea.
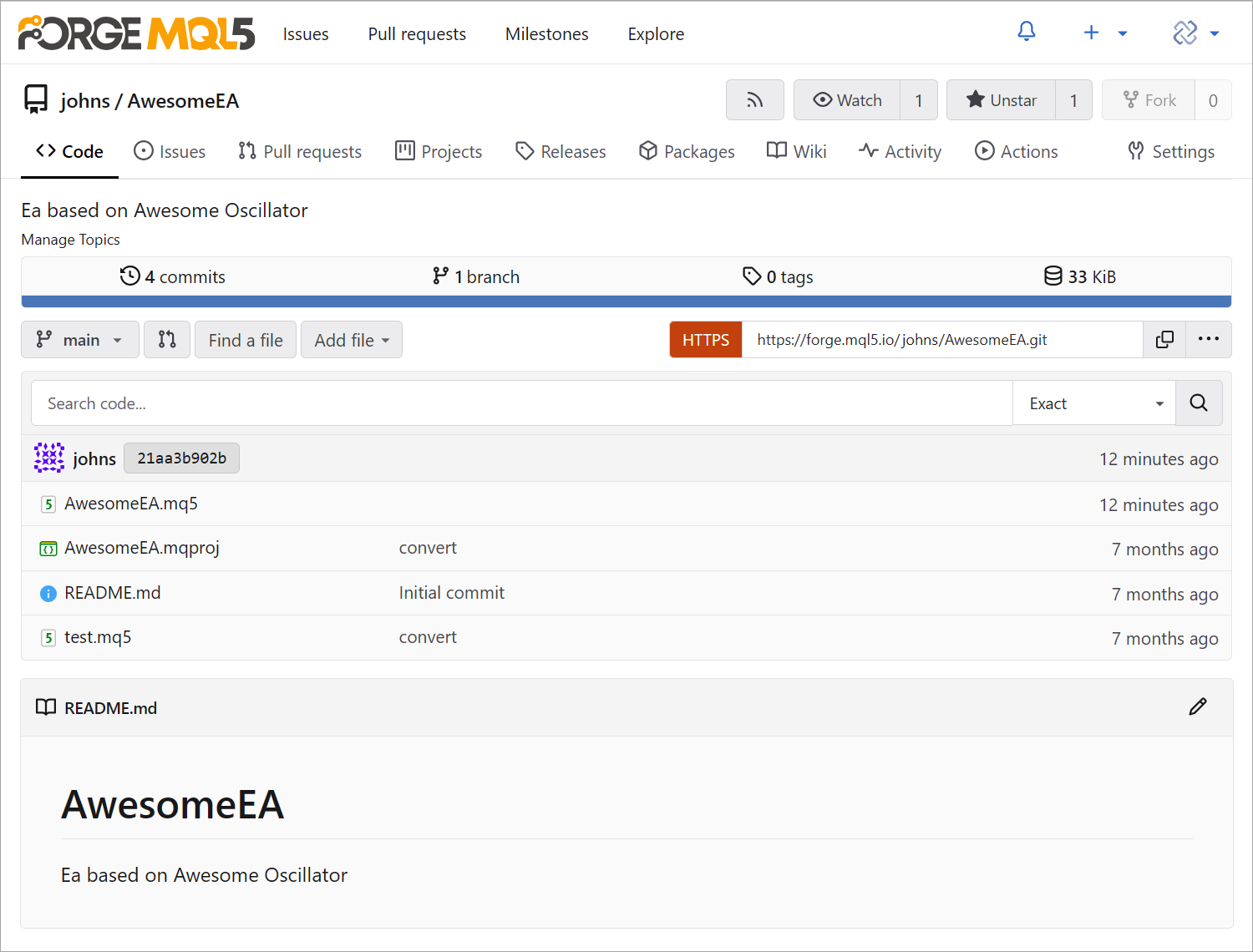
Lleve un registro de todos los cambios en el código: líneas nuevas, modificadas y eliminadas. Al detectar problemas, pida al desarrollador que los solucione directamente en el proyecto.
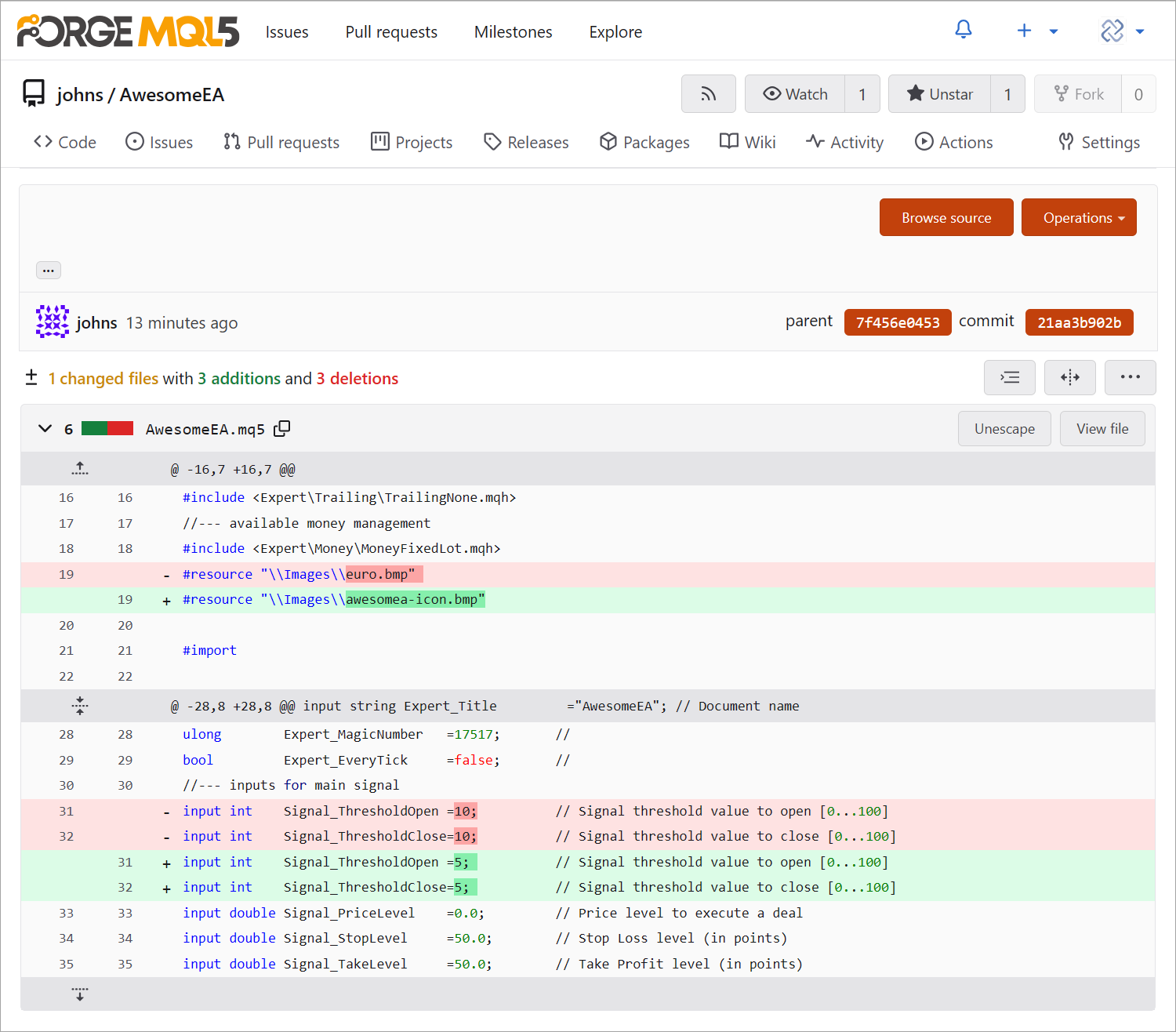
Para trabajar con Git, hemos rediseñado el menú Navegador y la ventana activa de edición de código. También hemos añadido un menú Git independiente al panel superior del MetaEditor:
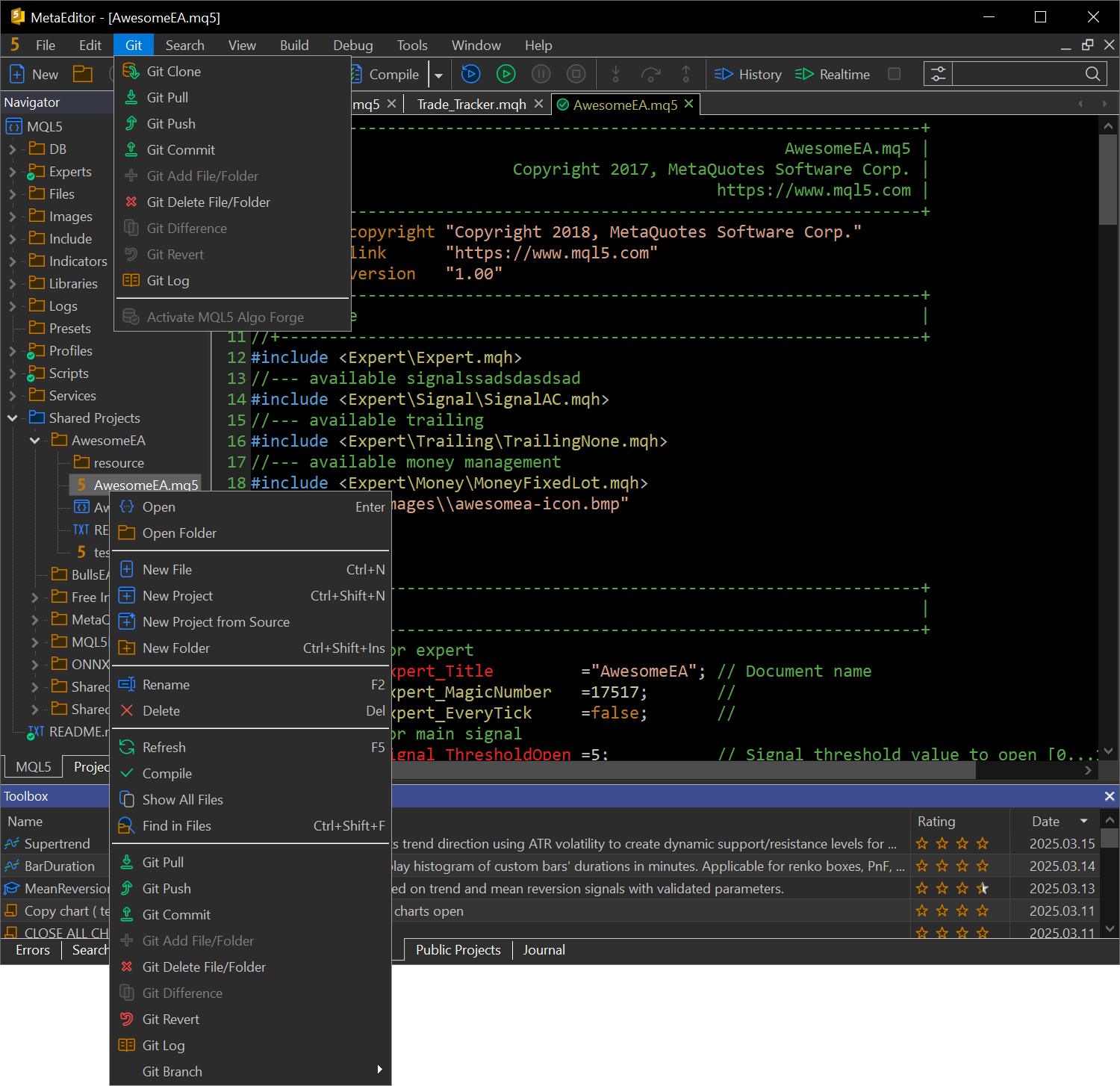
Todos los detalles sobre el trabajo con Git estarán pronto en la documentación.
Terminal
- Añadida la compatibilidad con el esquema de colores oscuros de la interfaz para todos los componentes: el terminal comercial, el MetaEditor y el simulador visual. El tema oscuro le permitirá trabajar con la plataforma más cómodamente por la noche. Utilice el menú «Ver» para cambiar al tema oscuro:
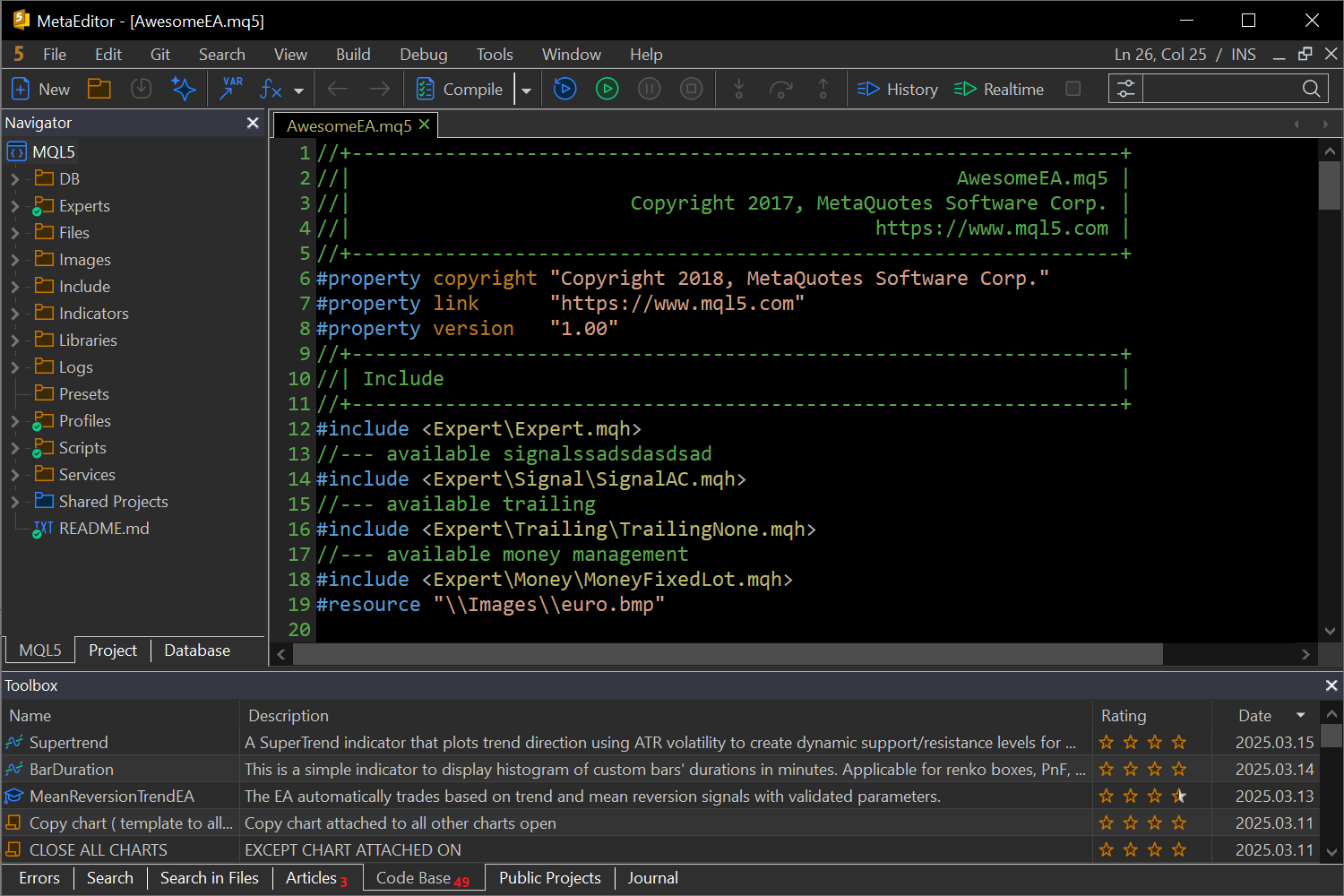
Adaptando la interfaz para que admita diferentes temas, hemos introducido muchas mejoras en la visualización de las ventanas de diálogo, menús, paneles y botones para que la experiencia resulte más cómoda. En el MetaEditor, la información sobre la posición actual del cursor en la ventana activa, así como el indicador del modo de entrada de texto (INS/OVR) se muestran en la esquina superior derecha. Para ahorrar espacio de trabajo, la barra de estado en la parte inferior de la ventana ya no se muestra.
- Añadida la posibilidad de alquilar un VPS durante 12 meses. Comprando el hosting de una sola vez y a largo plazo, ahorrará un tercio del coste.
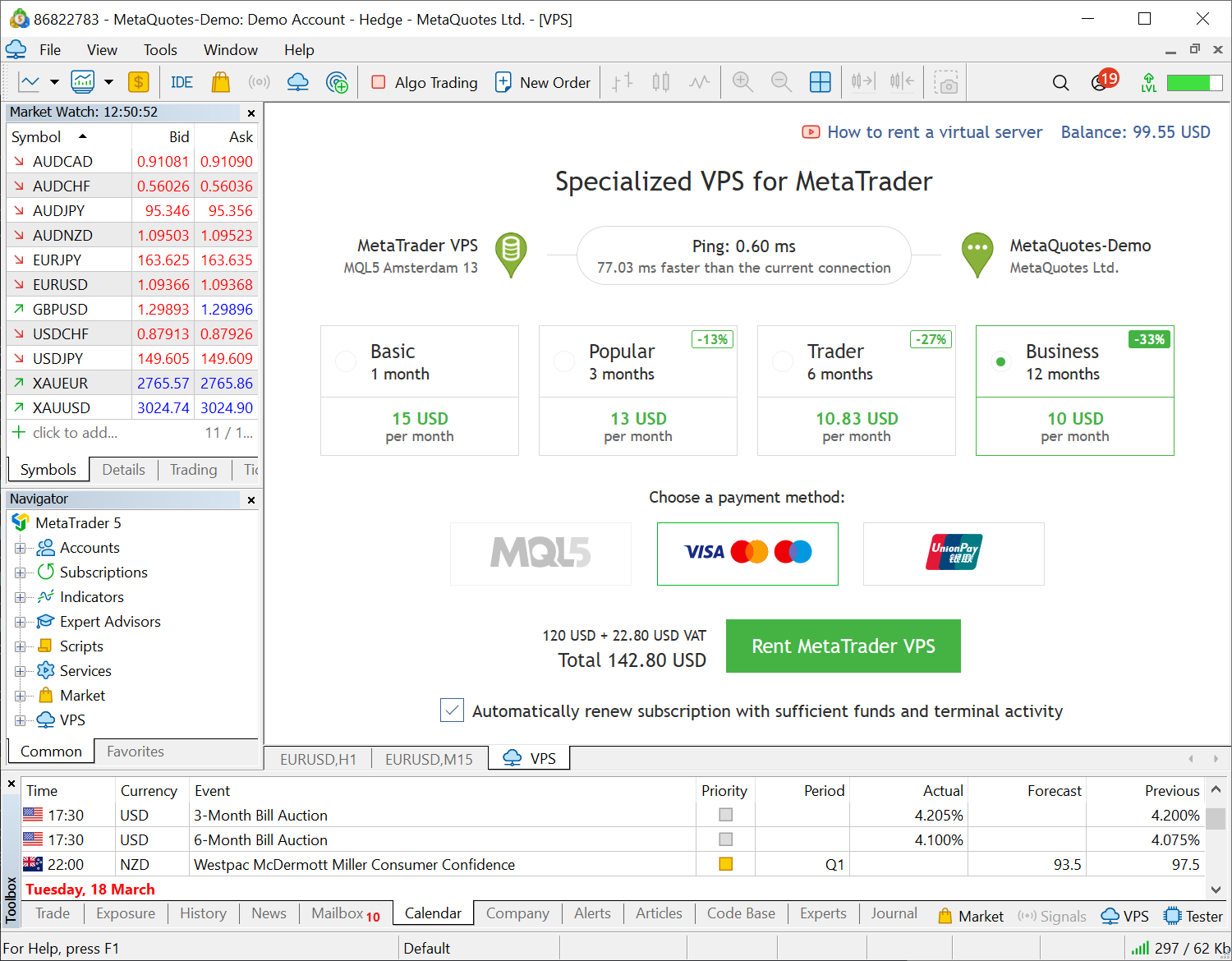
- Optimizado el consumo de memoria, ahora se utilizan menos recursos de la computadora para ejecutar el terminal.
- Optimizada la visualización de la historia comercial de la cuenta. Ahora la plataforma puede mostrar correctamente millones de entradas.
- Añadido el comando «Por defecto» al menú «Ventana». Este retorna todos los elementos de la interfaz (gráficos, Navegador, Simulador de estrategias, etc.) a su posición original.
- Corregido el error que, en algunos casos, provocaba el bloqueo de la ventana de diálogo de cambio de posición.
- Corregido el cálculo del coste de las posiciones abiertas al darse precios negativos.
- Corregido el cálculo del importe de garantía en las especificaciones de un instrumento comercial cuando se dan precios negativos.
- Corregido el cálculo de los valores actuales y la visualización de los gráficos MFE y MAE en el informe comercial.
- Corregido el escalado de los osciladores en las subventanas de los gráficos. La escala vertical de los mismos se muestra ahora correctamente.
- Corregida la ocultación y visualización de la profundidad de mercado y las tablas de opciones al cambiar al modo de pantalla completa.
- Añadida la visualización del ticket de la posición en la historia comercial de la cuenta. Utilice el menú contextual para activar la columna.
- Corregido el cálculo del valor de liquidación en la pestaña «Activos» para futuros y opciones.
- Corregido el copiado al portapapeles de los datos de las facturas creadas. En la última etapa del registro de una cuenta de demo o preliminar, el usuario obtiene los datos de la cuenta: el nombre de usuario, las contraseñas, etc. Estos se pueden copiar en el portapapeles para guardarlos en un archivo independiente. El comando correspondiente funciona ahora correctamente en macOS.
- Corregida la visualización de la sección de registro de VPS. En algunos casos, la página mostraba un error.
- Corregida la compatibilidad con monitores HiDPI al trabajar en Linux.
- Actualizadas las traducciones de la interfaz de usuario.
MQL5
- Añadido el operador de multiplicación de matrices @. Funciona según las reglas del álgebra lineal y permite multiplicar matrices y vectores, además de ejecutar el producto escalar de vectores.
Multiplicación de matrices (matriz × matriz)
matrix A(2, 3); matrix B(3, 2); matrix C = A @ B; // Resultado: matriz C con un tamaño [2,2]
Multiplicación de matrices (matriz × vector)
matrix M(2, 3); vector V(3); vector R = M @ V; // Resultado: vector R de 2 elementos
Multiplicación de matrices (vector × matriz)
matrix M(2, 3); vector V(1, 2); vector R = V @ M; // Resultado: vector R de 3 elementos
Producto escalar (vector × vector)
vector V1(1, 3), V2(1, 3); double r = V1 @ V2; // Resultado: escalar
- Añadido el parámetro ddof a los métodos Std, Var y Cov. Determina el número de grados de libertad que se restan del divisor al calcular la desviación típica. El parámetro por defecto para Std y Var será 0, y para Cov será 1.
Cómo influye el ddof:
- Por defecto, ddof=0 y la desviación típica se calcula para toda la población (desviación típica poblacional).
- Si ddof=1, se usará la desviación típica de la muestra, que ajustará la estimación para la muestra final (se utiliza en estadística al trabajar con un subconjunto de datos).
- Añadidos nuevos métodos OpenBLAS:
Cálculo de valores y vectores propios
- EigenTridiagonalDC — calcula los valores y vectores propios de una matriz simétrica tridiagonal utilizando el algoritmo «divide y vencerás» (función STEVD de LAPACK).
- EigenTridiagonalQR — calcula los valores y vectores propios de una matriz simétrica tridiagonal utilizando el algoritmo QR (función LAPACK de STEV).
- EigenTridiagonalRobust — calcula los valores y vectores propios de una matriz simétrica tridiagonal utilizando el algoritmo MRRR (Multiple Relatively Robust Representations) (función LAPACK de STEVR).
- EigenTridiagonalBisect — calcula los valores y vectores propios de una matriz simétrica tridiagonal utilizando el algoritmo de bisección (función LAPACK de STEVX).
- ReduceToBidiagonal — reduce una matriz general real o compleja de tamaño m×n a una forma bidiagonal superior o inferior B utilizando una transformación ortogonal: Q**T * A * P = B. Si m≥n, entonces B es una matriz bidiagonal superior, en caso contrario será una matriz bidiagonal inferior. (función GEBRD de LAPACK).
- ReflectBidiagonalToQP — genera matrices ortogonales Q y P**T (o P**H para tipos complejos) definidas por el método ReduceToBidiagonal al reducir la matriz real o compleja A a la forma bidiagonal: A = Q * B * P**T. Q y P**T son los productos de los reflectores elementales H(i) o G(i), respectivamente. (funciones LAPACK ORGBR, UNGBR).
- ReduceSymmetricToTridiagonal — reduce una matriz real simétrica o hermitiana compleja A a una forma tridiagonal B utilizando una transformación ortogonal de similitud: Q**T * A * Q = B. (funciones LAPACK SYTRD, HETRD).
- ReflectTridiagonalToQ — genera una matriz ortogonal Q, que es el producto de n-1 reflectores elementales de orden n devueltos por la función ReduceSymmetricToTridiagonal.
- LinearEquationsSolution — calcula un sistema de ecuaciones lineales con una matriz cuadrada de coeficientes A y varias partes derechas.
- LinearEquationsSolutionTriangular — calcula un sistema de ecuaciones lineales con una matriz triangular cuadrada de coeficientes A y múltiples partes derechas.
- LinearEquationsSolutionSy — calcula un sistema de ecuaciones lineales con matriz A simétrica o hermitiana conjugada y varias partes derechas.
- LinearEquationsSolutionComplexSy - calcula un sistema de ecuaciones lineales con matriz simétrica compleja A y varias partes derechas.
- LinearEquationsSolutionGeTrid — calcula un sistema de ecuaciones lineales con una matriz A simétrica o hermitiana conjugada definida positivamente y varias partes derechas.
- LinearEquationsSolutionSyPD — calcula un sistema de ecuaciones lineales con una matriz tridiagonal general (asimétrica) de coeficientes A y varias partes derechas.
- LinearEquationsSolutionSyTridPD — calcula un sistema de ecuaciones lineales con una matriz A simétrica tridiagonal definida positivamente y varias partes derechas.
- FactorizationQR — calcula la descomposición QR de una matriz general de tamaño m por n: A = Q * R (función LAPACK GEQRF).
- FactorizationQRNonNeg — calcula la descomposición QR de una matriz general de tamaño m por n: A = Q * R, donde R es una matriz triangular superior con elementos no negativos en la diagonal (función LAPACK GEQRFP).
- FactorisationQRPivot — calcula la descomposición QR de una matriz general de tamaño m por n con permutación de columnas: A * P = Q * R (función LAPACK GEQP3).
- FactorisationLQ — realiza una descomposición LQ de una matriz general de tamaño m en n: A = L * Q (función LAPACK de GELQF).
- FactorisationQL — realiza una descomposición QL de una matriz general de tamaño m en n: A = Q * L (función LAPACK de GEQLF).
- FactorisationRQ — realiza una descomposición RQ de una matriz general de tamaño m en n: A = R * Q (función LAPACK de GERQF).
- FactorizationPLU — calcula la descomposición LU de una matriz general A de tamaño m por n usando la selección parcial del elemento principal y permutaciones de filas (función LAPACK GETRF).
- FactorizationPLUGeTrid — calcula la descomposición LU de una matriz tridiagonal general (asimétrica) A de tamaño n por n utilizando la selección parcial del elemento principal y permutaciones de filas (función LAPACK de GTTRF).
- FactorizationLDL — calcula la descomposición de una matriz real simétrica o hermitiana compleja A utilizando la selección diagonal del elemento principal por el método de Bunch-Kaufman (funciones LAPACK SYTRF y HETRF).
- FactorizationLDLSyTridPD — calcula la descomposición de una matriz tridiagonal A simétrica definida positivamente (para datos reales) o hermitiana definida positivamente (para datos complejos) (función LAPACK PTTRF).
- FactorizationCholesky — calcula la descomposición para una matriz real simétrica o hermitiana compleja positiva-definida A (función LAPACK POTRF).
- FactorizationCholeskySyPS — calcula la descomposición de Cholesky con pivoteo completo para una matriz real simétrica (o hermitiana compleja) positiva semidefinida A de tamaño n por n (función LAPACK PSTRF).
- Añadida la función y el método Random para rellenar vectores y matrices con valores aleatorios. Los valores aleatorios se generan uniformemente dentro del rango establecido.
static vector vector::Random( const ulong size, // longitud del vector const double min=0.0, // valor mínimo const double max=1.0 // valor máximo ); static matrix matrix::Random( const ulong rows, // número de filas const ulong cols // número de columnas const float min=0.0, // valor mínimo const float max=1.0 // valor máximo );
- Añadido soporte para pseudónimos adicionales de tipo entero. Esto facilitará la portabilidad de código de otros lenguajes, como C y C++.
Estos pseudónimos no introducen nuevos tipos, sino que son nombres alternativos de tipos ya existentes en MQL5. Pueden utilizarse en todos los contextos en los que son aplicables los tipos básicos.
- int8_t
- uint8_t
- int16_t
- uint16_t
- int32_t
- uint32_t
- int64_t
- uint64_t
- Añadidas funciones para definir el esquema de colores del terminal:
- Nueva propiedad TERMINAL_COLORTHEME_NAME en la enumeración ENUM_TERMINAL_INFO_STRING. Utilícela para consultar el tipo de esquema de colores mediante la función TerminalInfoString. Valores posibles: Light y Dark.
- Nuevas propiedades THEME_COLOR_* en la enumeración ENUM_TERMINAL_INFO_INTEGER. Utilícelas para obtener los colores de elementos específicos de la interfaz mediante la función TerminalInfoInteger.
Utilice el manejador OnChartEvent para determinar si el esquema de color ha cambiado. El evento CHARTEVENT_CHART_CHANGE se llama dos veces al cambiar el patrón. - Corregido el error que provocaba que MetaEditor se bloqueara al compilar código con el método Array::Reserve. El método Reserve no cambia el tamaño del array, sino que reserva espacio para el número especificado de elementos para evitar la sobreasignación de memoria al añadir nuevos elementos.
- Corregido el método Array::Push que añade nuevos elementos al final del array. El error se producía en los arrays que tenían una reserva en el búfer.
- Corregidas las funciones para trabajar con OpenCL.
MetaTester
- Acelerada la optimización de las estrategias comerciales.
- Corregido el error que en algunos casos provocaba un consumo excesivo de RAM por parte de los agentes de prueba al ejecutar tareas desde la red MQL5 Cloud Network.
Terminal web
- Corregida la opción de guardar contraseña en la ventana de diálogo de conexión de cuentas.
- Corregido el funcionamiento de los botones para desplazar el gráfico. En algunos casos, al usar estos, el gráfico podía desaparecer.
- Corregida la validación del campo «Patronímico» en el formulario de solicitud de cuentas reales. Ahora no es obligatorio rellenarlo.
- Corregida la apertura de cuentas demo. En algunos casos, al abrir una cuenta, se daba un redireccionamiento incorrecto al sitio web del bróker.
- Corregida la visualización de los botones de apertura de cuentas demo y reales. Ahora los botones están ocultos si la función correspondiente ha sido desactivada por el bróker.
- Corregido el funcionamiento del campo «Depósito» en el formulario de apertura de cuentas demo.
- Corregida la visualización del campo «Trading» en las especificaciones del contrato.
- Corregido el campo de búsqueda de símbolos en la ventana «Observación del mercado». Ahora muestra un botón «X» para salir del modo de búsqueda.
- Corregida la información sobre herramientas del campo en el que se introduce el código de confirmación de correo electrónico en el formulario de apertura de cuenta.
En las últimas versiones de la aplicación móvil MetaTrader 5 para iOS, hemos añadido muchas características cómodas para los gráficos, y también hemos realizado varias correcciones importantes para que la aplicación funcione de forma más estable.
- Añadido un objeto de texto para crear rótulos personalizados en el gráfico. Vaya al menú de objetos del gráfico y haga clic en "Añadir texto". A continuación, introduzca el texto y seleccione el punto del gráfico en el que deberá colocarse. El objeto tendrá dos puntos: para desplazarse y para cambiar de dirección.
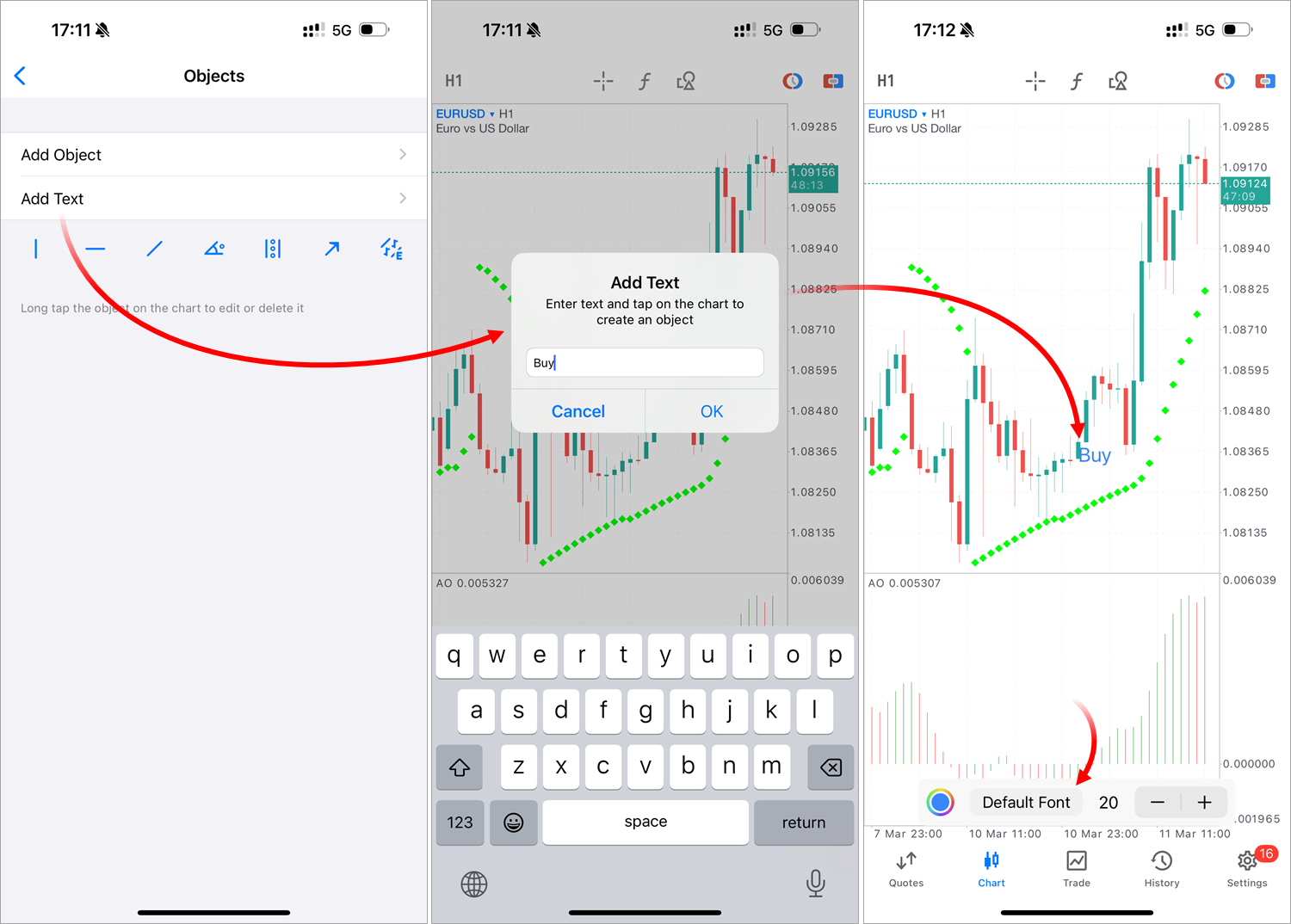
También hemos añadido al gráfico un pequeño menú de objetos: aparecerá en la parte inferior en cuanto estos sean creados. Ahora no tendrá que ir al menú del objeto para cambiar las propiedades básicas. - Añadido un temporizador que muestra el tiempo hasta el final de la barra actual. Funciona en todos los marcos temporales, permitiéndonos seguir cualquier vela, desde velas diminutas hasta velas diarias. La función resultará útil para aquellos tráders cuyas estrategias se basen en barras de cierre o apertura.
Para activar el temporizador, vaya a la configuración del gráfico. La hora se mostrará en la escala vertical, debajo del precio actual.
- Mejorado el modo de retícula: ahora se podrá utilizar como regla. Active la retícula y colóquela sobre el punto deseado a partir del cual desea medir la distancia. A continuación, clique una vez en el punto hasta el que desea medir la distancia. La diferencia de precio, el porcentaje y el número de barras se mostrarán en la sugerencia.

- Añadida la visualización del ticket de la posición en la historia comercial.
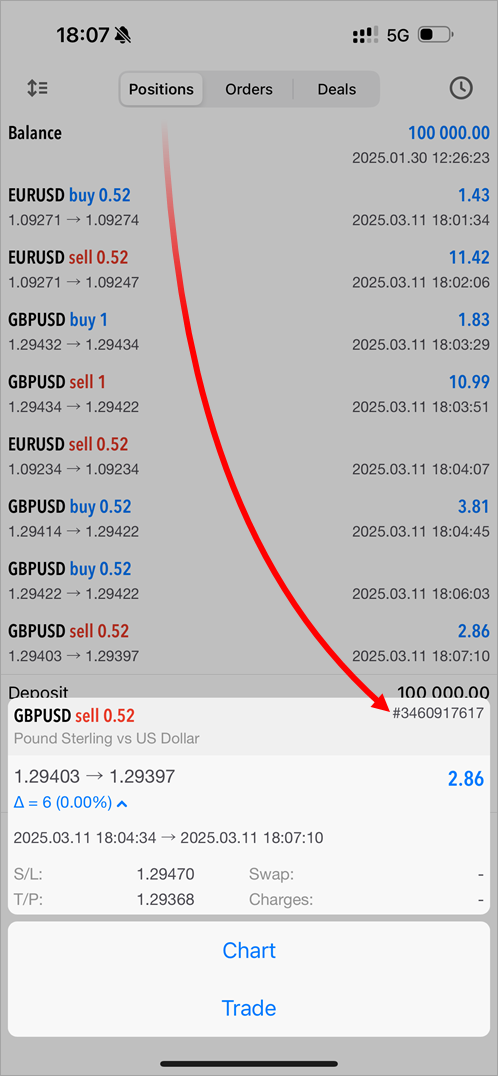
- Mejorada la visualización del retraso de las cotizaciones, si existe, para el instrumento comercial. Ahora la información se indicará ahora en el gráfico, mientras que el icono en la Observación de Mercado será más notorio.
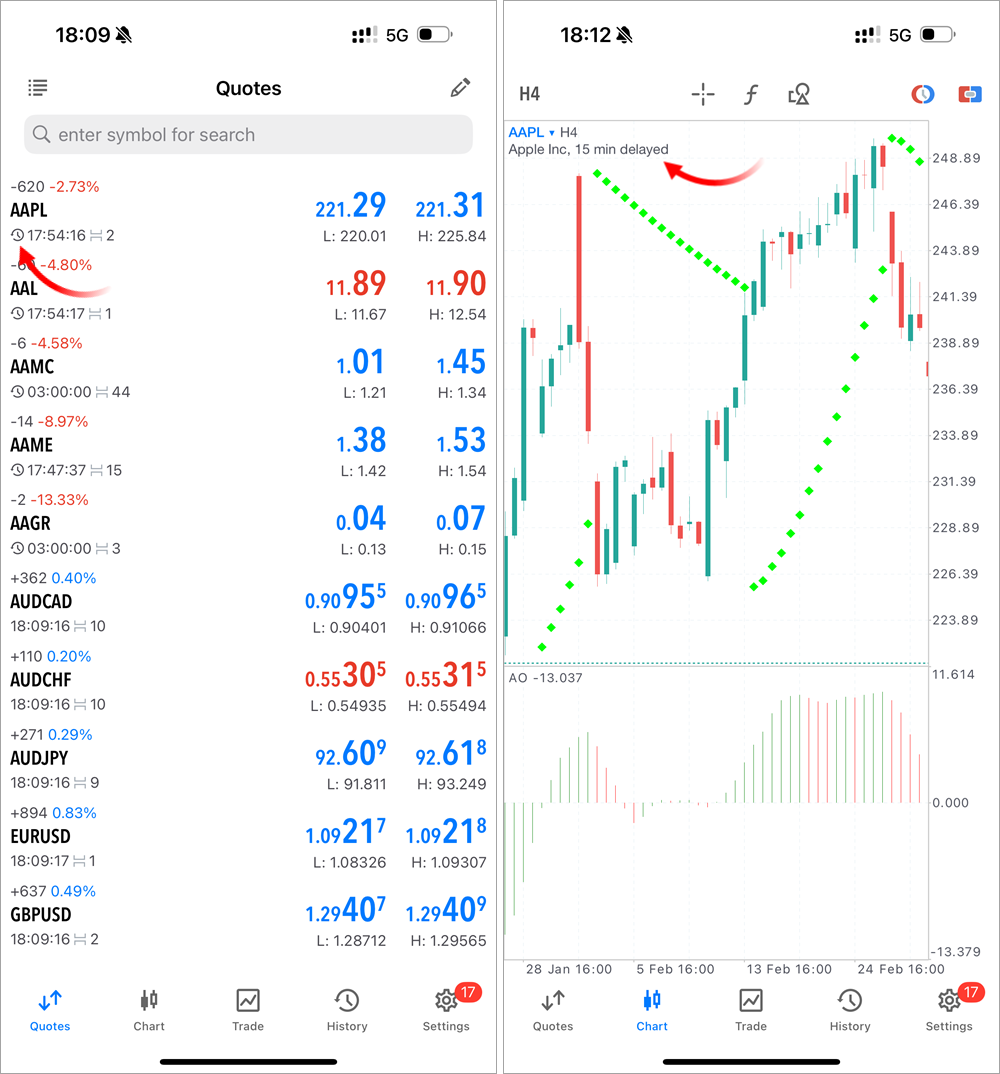
- Añadido el soporte para nuevos proveedores para el sistema de pago incorporado.
- Añadido un campo para introducir la fecha de nacimiento al abrir cuentas demo.
- Mejoradas las salas de chat: hemos corregido la visualización de avatares, hemos añadido el visor de documentos y corregido la compatibilidad con imágenes *.webp, además de la búsqueda.
Instale la última versión de la aplicación y amplíe sus posibilidades comerciales:
 |
Terminal
- Terminal: Modificado
el cálculo del coste de las posiciones, órdenes y transacciones. Ahora
se muestra en la divisa de depósito de la cuenta y no en la divisa
básica del instrumento comercial:

- Terminal: Añadido un campo para introducir la fecha de nacimiento al abrir cuentas demo.
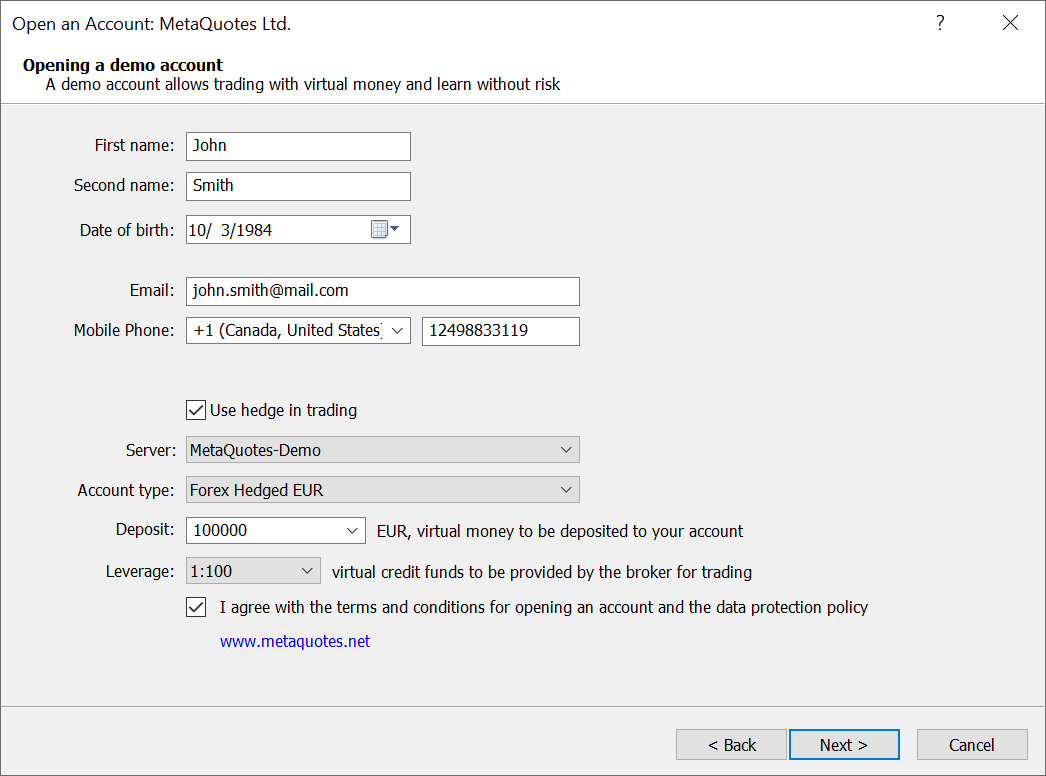
- Terminal: Corregida la escala de los indicadores mostrados en la subventana del gráfico. Para algunos osciladores, los valores de escala mínimo y máximo podían seleccionarse incorrectamente.
- Terminal: Optimizado y acelerado el análisis de los datos de ticks y la historia de precios, lo que aumentará la velocidad de apertura de los gráficos.
- Terminal: Corregida la edición del color del texto en la ventana de creación de correo interno
- Terminal: Actualizadas las traducciones de la interfaz de usuario.
MQL5
- Añadidos nuevos métodos OpenBLAS:
- EigenSolver2 — cálculo de valores propios y vectores propios generalizados para un par de matrices cuadradas ordinarias (función lapack GGEV).
- EigenSolverX — cálculo de valores propios y vectores propios de una matriz cuadrada regular en el modo de Experto (Expert mode), es decir, con la posibilidad de influir en el algoritmo de cálculo y la posibilidad de obtener los datos de cálculo asociados (función lapack GEEVX).
- EigenSolver2X — cálculo de valores propios generalizados y vectores propios para un par de matrices cuadradas ordinarias en el modo de Experto (Expert mode), es decir, con la posibilidad de influir en el algoritmo de cálculo y la posibilidad de obtener los datos de cálculo asociados (función lapack GGEVX).
- EigenSolverShur — cálculo de valores propios, matriz triangular superior en forma de Schur y matriz de vectores de Schur (función lapack GEES).
- EigenSolver2Shur — cálculo para un par de matrices cuadradas ordinarias de valores propios generalizados, vectores propios generalizados, formas de Schur generalizadas y vectores de Schur izquierdo y derecho (función lapack GGES).
- EigenSolver2Blocked — cálculo de valores propios generalizados y vectores propios para un par de matrices cuadradas ordinarias utilizando el algoritmo de bloques (función lapack GGEV3).
- EigenSolver2ShurBlocked — cálculo para un par de matrices cuadradas ordinarias de valores propios generalizados, vectores propios generalizados, formas de Schur generalizadas y vectores de Schur izquierdo y derecho utilizando el algoritmo de bloques (función lapack GGES3).
- EigenSymmetricRobust — cálculo de valores propios y vectores propios de una matriz simétrica o hermitiana (conjugada compleja) utilizando el algoritmo MRRR de representaciones múltiples relativamente robustas (funciones lapack SYEVR, HEEVR).
- EigenSymmetricBisect — cálculo de valores propios y vectores propios de una matriz simétrica o hermitiana (conjugada compleja) utilizando el algoritmo de bisección (funciones lapack SYEVX, HEEVX).
- Añadidos nuevos métodos para matrices complejas:
- TransposeConjugate — para crear una matriz conjugada-transpuesta.
matrix<complex<T>> matrix<complex<T>>::TransposeConjugate(void) const;
El método retorna una nueva matriz conjugada-transpuesta en la que los elementos de la matriz original se transponen y reducen a sus valores conjugados complejos.
Si ocurre un error, se retornará una matriz vacía; para obtener el código de error, use la función GetLastError;
- CompareEqual — comparación absoluta de dos matrices.
int matrix<T>::CompareEqual(const matrix<T>& mat) const
Valores de retorno:
- -1 — si el elemento de la matriz A es menor que el elemento correspondiente de la matriz B.
- 0 — si todos los elementos de las matrices A y B son idénticos.
- 1 — si el elemento de la matriz A es mayor que el elemento correspondiente de la matriz B.
El método también puede retornar errores si el estado de los datos de entrada es incorrecto. Para obtener el código de error, utilice la función GetLastError.
- TransposeConjugate — para crear una matriz conjugada-transpuesta.
- Añadido soporte para Python hasta la versión 3.13 para el paquete de integración correspondiente. Para actualizar el paquete, ejecute el comando:
pip install --upgrade MetaTrader5
- Corregida la omisión del primer evento Timer. El error se producía si el temporizador estaba activado dentro del manejador OnTimer.
MetaEditor
- Corregido el cálculo de valores para las variables de entrada cuando se trabaja con el depurador. En algunos casos, se mostraba el mensaje unknown identifier en lugar del valor.
Tester
- Corregida la
búsqueda de los tipos de cambio cruzado necesarios para la conversión de
divisas al realizar pruebas en instrumentos bursátiles.
Terminal web
- Añadido soporte para el modo de ejecución «Por pedido» para órdenes de gran volumen.
- Añadido soporte para una descripción extendida del motivo por el que el bróker ha rechazado una solicitud.
- Corregido el formulario de apertura de cuenta. Ahora el conjunto de datos solicitados coincidirá con la configuración del bróker.
- Corregida la detección del país al registrar una cuenta demo.
- Corregida la alineación de la ventana de diálogo con la advertencia sobre la habilitación del trading con un solo clic.
Terminal
- Corregido el error que provocaba que, en algunos casos, se solicitara una historia de ticks incompleta.
- Corregido el autocompletado al seleccionar caracteres para idiomas distintos del inglés. Cuando el usuario introduce el nombre de un carácter en la casilla de búsqueda, el sistema comenzará a sugerir automáticamente opciones adecuadas. Ahora la búsqueda funciona correctamente y no distinguirá entre mayúsculas y minúsculas en todas las configuraciones regionales.
MQL5
- Añadida la descripción de los nuevos métodos OpenBLAS a la documentación de MQL5. Hasta ahora se han añadido 15 nuevos métodos para matrices y vectores, y estamos trabajando para completarlos.
OpenBLAS es una eficaz solución de código abierto para la computación de alto rendimiento, especialmente al trabajar con grandes conjuntos de datos.Función
Acción
Singular Value Decomposition, algoritmo divide and conquer. Se considera el más rápido entre otros algoritmos SVD (función lapack de GESDD).
Singular Value Decomposition, algoritmo QR. Se considera un algoritmo SVD clásico (función lapack de GESVD).
Singular Value Decomposition, algoritmo QR with pivoting ( función lapack de GESVDQ).
Singular Value Decomposition, algoritmo bisection (función lapack de GESVDX).
Singular Value Decomposition, algoritmo Jacobi high level (función lapack de GEJSV).
Singular Value Decomposition, algoritmo Jacobi low level (función lapack de GESVJ). En algunos casos, calcula valores singulares pequeños y sus vectores singulares con mucha más precisión que otras rutinas SVD.
Singular Value Decomposition, algoritmo divide and conquer para una matriz bidiagonal (función lapack de BDSDC).
Singular Value Decomposition, algoritmo bisection para matrices bidiagonales ( función lapack de BDSVDX).
Cálculo de los valores y vectores propios de una matriz cuadrada ordinaria usando el algoritmo clásico (función lapack de GEEV).
Cálculo de los valores y vectores propios de una matriz simétrica o hermitiana (conjugada compleja) usando el algoritmo divide and conquer (funciones lapack de SYEVD, HEEVD).
Función de método para calcular las contribuciones relativas de los componentes espectrales a partir de los valores propios.
Función de método para calcular datos reconstruidos y predichos utilizando componentes espectrales de las series temporales de entrada.
Función de método para calcular los componentes reconstruidos de las series temporales de entrada y sus contribuciones.
Función de método para calcular una serie temporal reconstruida utilizando los primeros componentes de component_count.
- Corregidos los errores que sucedían al iniciar versiones antiguas de archivos ejecutables MQL5 (archivos .ex5) que utilizan métodos matrix::CopyRates. Estos errores no se producían en los archivos compilados después de instalar las actualizaciones necesarias.
- Corregida la comprobación de los tipos de objetos permitidos en union.
MetaTester
- Corregidos los fallos que se producían en algunos casos al desinicializar indicadores personalizados.
Terminal
- Corregidos los fallos que se producían en algunos casos al detener el perfilado de programas MQL5.
MetaEditor
- Corregidas las fugas de memoria durante la compilación de programas MQL5 y durante el funcionamiento de las funciones de administración intelectual del código.
MetaTester
- Corregidos los fallos que se producían en algunos casos al reiniciar una sola pasada de prueba.
Terminal
- Limitado el acceso a las funciones de MQL5 para el
comercio y la obtención de la historia cuando existe una suscripción a
una señal en la cuenta.
Al detectarse una suscripción en la cuenta (no importa si el copiado está activado en el terminal actual), se prohibirá llamar a cualquier función comercial de MQL5: obtener las órdenes y posiciones abiertas, obtener la historia, realizar operaciones comerciales. La advertencia correspondiente aparecerá en el diario de registro:'XXX': signal subscription detected, trading and history access functions in MQL5 and Python disabledLas restricciones también se aplicarán a las llamadas de las funciones comerciales de Python: positions_total, positions_get, orders_total, orders_get, history_orders_total, history_orders_get, history_deals_total, history_deals_get, order_check, order_send.
Si la cuenta se da de baja de la señal o usted se conecta a otra cuenta que no esté suscrita a la señal, se eliminará la restricción y aparecerá un mensaje en el diario de registro:'XXX': no signal subscription detected, trading and history access functions in MQL5 and Python enabledSi existen restricciones en la cuenta, las funciones MQL5 retornarán los siguientes códigos de respuesta:
- OrderSend, OrderSendAsync — RET_REQUEST_AT_DISABLED_CLIENT
- OrdersTotal, PositionsTotal — 0
- PositionGetSymbol, PositionSelect, PositionSelectByTicket, PositionGetTicket — ERR_MQLAPI_TRADE_POSITION_NOT_FOUND
- OrderGetTicket, OrderSelect — ERR_MQLAPI_TRADE_POSITION_NOT_FOUND
- HistorySelect — retorna ERR_MQLAPI_TRADE_DEAL_NOT_FOUND
- Corregida, optimizada y acelerada sustancialmente la consulta de la historia de ticks y su exportación a archivos CSV/HTML.
- Añadida compatibilidad con Microsoft Edge WebView2 para representar páginas HTML en la plataforma comercial en macOS.
En comparación con el MSHTML, ya obsoleto, el nuevo componente amplía
enormemente las posibilidades de muestra de contenido web, ofreciendo
acceso a tecnologías modernas. El cambio a WebView2 ha mejorado el
aspecto de las secciones «Mercado», «Señales», «VPS», etc., ha aumentado
su rendimiento y ha creado interfaces más receptivas.
- Menú contextual fijo en la ventana de envío de correos electrónicos a través del correo incorporado.
- Corregido el filtrado en la ventana de diálogo de la selección de instrumentos comerciales. Ahora ya no tendrá que escribir primero su nombre en la barra de búsqueda para ocultar los instrumentos que han expirado.
- Corregido el cálculo de la garantía prevista (requisitos de margen) en la ventana de especificación del contrato. El error surgía en los instrumentos del tipo Exchange Stocks y Bonds.
- Mejorada la función de cierre masivo de posiciones comerciales para las cuentas con FIFO. Ahora no se mostrarán para ellas los tipos de transacciones incompatibles: cierre de todas las posiciones rentables/con pérdidas, posiciones en una dirección y posiciones opuestas.
- Corregido el error que impedía a los usuarios colocar órdenes pendientes multidireccionales en cuentas cuyas posiciones se cierran utilizando la regla FIFO.
- Corregido el cálculo fijo del valor de liquidación de una cuenta comercial cuando existen posiciones en instrumentos con el tipo Exchange Futures.
- Corregido el cálculo fijo del beneficio flotante para posiciones en instrumentos con el tipo Exchange Bonds y Exchange MOEX Bonds.
- Desactivada la función de creación automática de cuentas demo al iniciar la plataforma si no hay cuentas añadidas previamente.
- Mejorado el control sobre el nombre y el correo electrónico introducidos al registrar las cuentas.
- Corregido el cálculo del margen para las posiciones cubiertas. El error podría producirse en algunos casos cuando se utilizaba margen flotante en la cuenta (dependiendo del volumen/valor de las posiciones en la cuenta).
- Corregida la actualización del estado del botón "Siguiente" en la
ventana de diálogo de apertura de una cuenta demo. Después de introducir
el código de confirmación por teléfono o por correo electrónico, el
botón podía quedar inactivo.
- Actualizadas las traducciones de la interfaz de usuario.
MQL5
- Añadida integración nativa con la biblioteca de cálculo matricial OpenBLAS.
OpenBLAS es una biblioteca de álgebra lineal de código abierto y alto rendimiento que implementa BLAS (Basic Linear Algebra Subprograms) y algunas funciones de LAPACK. OpenBLAS pretende mejorar el rendimiento computacional, especialmente en operaciones matriciales y cálculos vectoriales que resultan importantes en tareas científicas y de ingeniería como el aprendizaje automático, los métodos numéricos y las simulaciones.
Las principales características de OpenBLAS son:- Soporte multihilo: OpenBLAS puede usar eficazmente varios núcleos de procesador para la computación paralela, lo cual acelera considerablemente las operaciones en sistemas multiprocesador.
- Optimización para arquitecturas de procesador: OpenBLAS incluye versiones optimizadas para varios procesadores como Intel, AMD, ARM y otros. La biblioteca detecta automáticamente las características del procesador (conjuntos de instrucciones AVX/AVX2/AVX512 compatibles) y elige las implementaciones de funciones más adecuadas.
- Soporte para una amplia gama de operaciones BLAS: OpenBLAS implementa funciones BLAS básicas como operaciones con vectores (por ejemplo, suma de vectores y producto escalar), matrices (multiplicación) y operaciones vector-matriz.
- Compatibilidad con LAPACK: la biblioteca soporta una serie de funciones LAPACK (Linear Algebra PACKage), necesarias para operaciones de álgebra lineal más complejas, como la resolución de sistemas de ecuaciones lineales, el cálculo de valores propios de matrices y otras.
- Alto rendimiento: en comparación con otras bibliotecas BLAS, OpenBLAS suele ofrecer un mejor rendimiento gracias a la optimización manual de arquitecturas de procesador específicas.
OpenBLAS se usa ampliamente en aplicaciones relacionadas con la computación numérica, como:- El entrenamiento de redes neuronales y otras tareas de aprendizaje automático.
- La informática científica (por ejemplo, modelización de procesos físicos).
- El manejo y análisis de grandes cantidades de datos.
Los siguientes métodos están disponibles actualmente en MQL5:
Descomposición singular:- SingularValueDecompositionDC es un algoritmo divide and conquer. Se considera el más rápido entre otros algoritmos SVD (función lapack de GESDD).
- SingularValueDecompositionQR es un algoritmo QR. Se considera un algoritmo SVD clásico (función lapack de GESVD).
- SingularValueDecompositionQRPivot es un algoritmo QR with pivoting (función lapack de GESVDQ).
- SingularValueDecompositionBisect es un algoritmo bisection (función lapack de GESVDX).
- SingularValueDecompositionJacobiHigh es un algoritmo Jacobi de alto nivel (función lapack GEJSV).
- SingularValueDecompositionJacobiLow es un algoritmo Jacobi de bajo nivel (función lapack de GESVJ). En algunos casos, calcula valores singulares pequeños y sus vectores singulares con mucha más precisión que otras rutinas SVD.
- SingularValueDecompositionBidiagDC es un algoritmo divide and conquer para matrices bidiagonales (función lapack BDSVDX).
- SingularValueDecompositionBidiagBisect es un algoritmo bisection para matrices bidiagonales (función lapack de BDSVDX).
- EigenSolver supone el cálculo de los valores y vectores propios de una matriz cuadrada ordinaria mediante el algoritmo clásico (función lapack de GEEV).
- EigenSymmetricDC supone el cálculo de valores y vectores propios de una matriz simétrica o hermítica (compleja-conjugada) utilizando el algoritmo divide and conquer (funciones lapack de SYEVD, HEEVD).
En breve dispondrá de documentación detallada.
- Añadido el valor SYMBOL_SWAP_MODE_CURRENCY_PROFIT a la enumeración ENUM_SYMBOL_SWAP_MODE. Si la función SymbolInfoInteger retorna un valor de este tipo, significa que los swaps de la cuenta se acumularán en dinero en la divisa de cálculo del beneficio.
- Ampliada la compatibilidad con ONNX Runtime. Añadidos nuevos tipos de operaciones de aprendizaje automático que permiten ejecutar modelos neuronales más complejos.
- La transición a un compilador MQL5 más eficaz sigue progresando. Ya se usa para parte de las funciones. La transición permitirá usar nuevas optimizaciones y aumentar la velocidad de ejecución de los programas.
- Añadidos nuevos tipos de datos necesarios para soportar la biblioteca OpenBLAS:
- complexf - número complejo con datos float
- vectorcf - vector que contiene elementos de tipo complexf
- matrixcf - matriz que contiene elementos de tipo complexf
- Mejorado el funcionamiento de WebRequest al trabajar con sitios web que infringen las normas de formación de URL, tienen errores de redirección o grandes listas de nombres DNS alternativos.
- Corregida la asignación simultánea a varias variables de tipo matrix o vector.
MetaEditor
- Actualizados los modelos disponibles para el AI Assistant. Ahora se usará el GPT-4o mini, más moderno, en lugar del GPT-3.5 Turbo. También se ha añadido el modelo 01-mini.
- Corregido un error en el depurador que, en algunos casos, provocaba que los valores de las variables no se actualizaran en la ventana de observación.
- Actualizadas las traducciones de la interfaz de usuario.
MetaTester
- Corregido el guardado de los coeficientes de margen en los ajustes personalizados de los símbolos.
- Corregidas las fugas de memoria que se producían en algunos casos entre pasadas de prueba.
Terminal web
- Añadido el modo «Retícula» para ver valores exactos y medir distancias en el gráfico.
Haga clic en el botón correspondiente del panel izquierdo. Pase la retícula por encima de cualquier punto del gráfico: la fecha y el precio se mostrarán en las escalas correspondientes. Para medir la distancia, haga clic en cualquier punto del gráfico y desplace el cursor a otro punto sin soltar el botón del ratón.
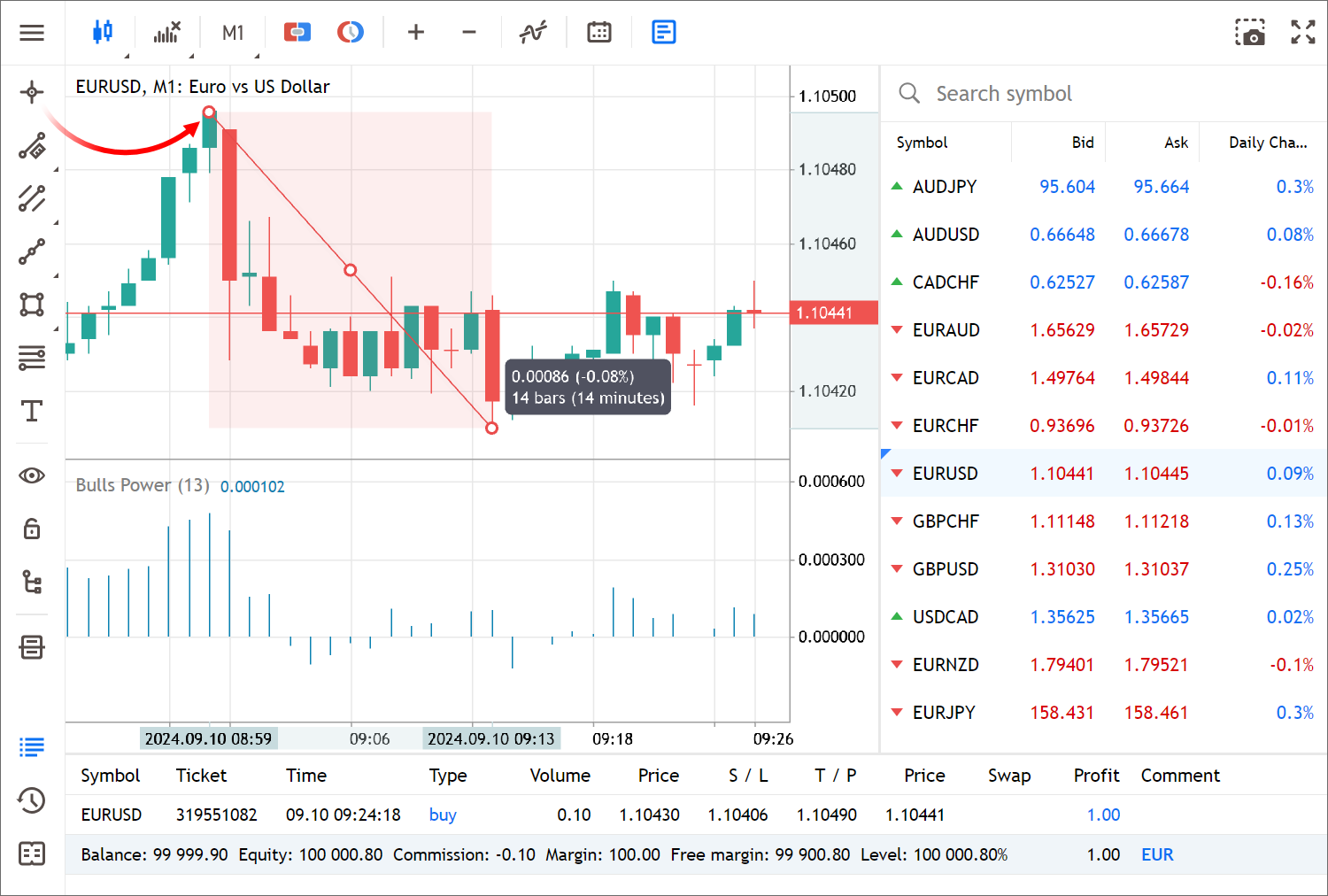
También podrá utilizar teclas de acceso rápido: el botón central del ratón para activar la retícula, y Esc o el botón derecho del ratón para desactivarla.
- Añadida la representación del gráfico como una línea simple trazada por los precios de cierre de las barras:
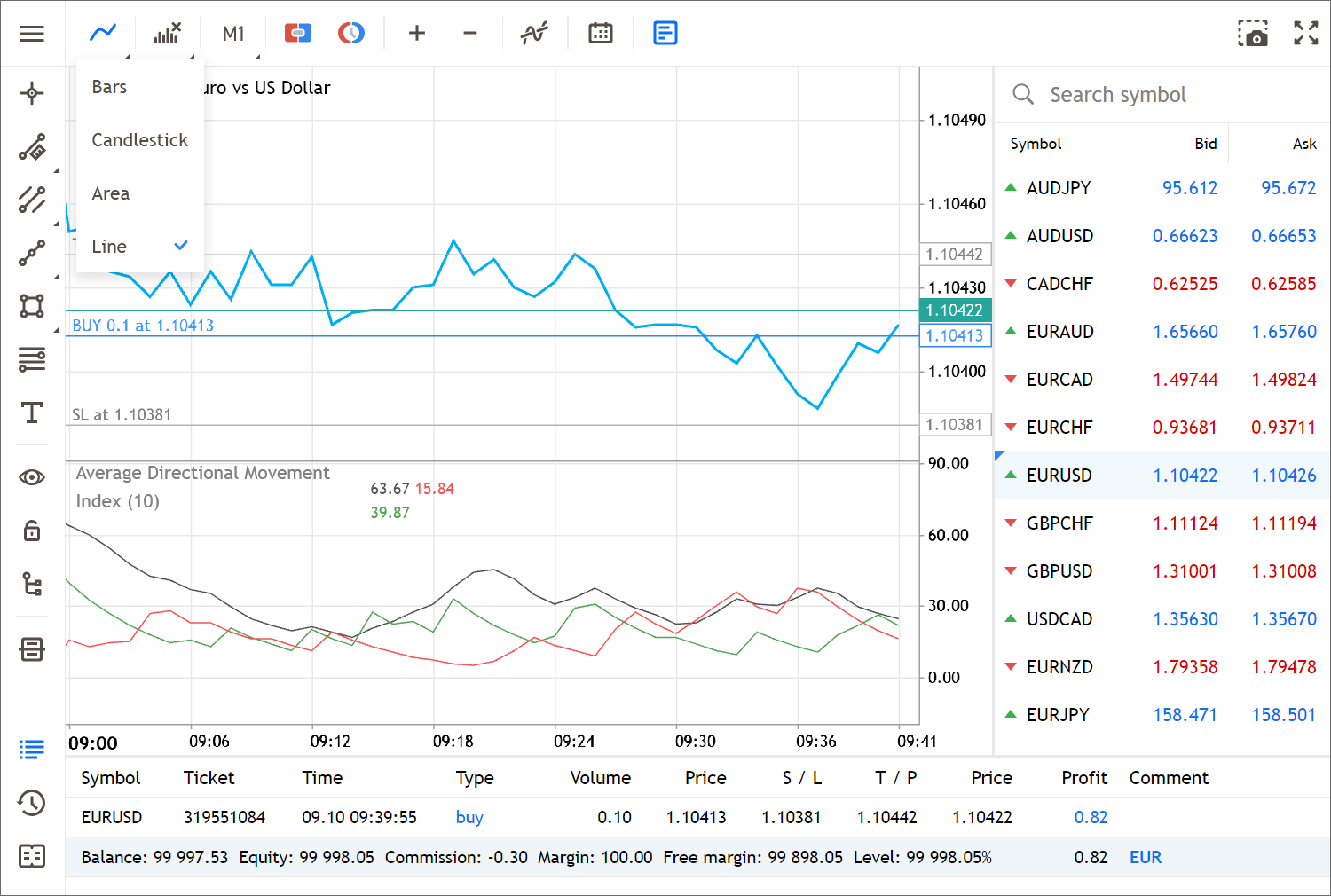
- Añadida la posibilidad de mostrar columnas adicionales en la
«Observación de mercado» en la vista móvil. Para configurar, vaya al
modo tabular y pulse «...»:
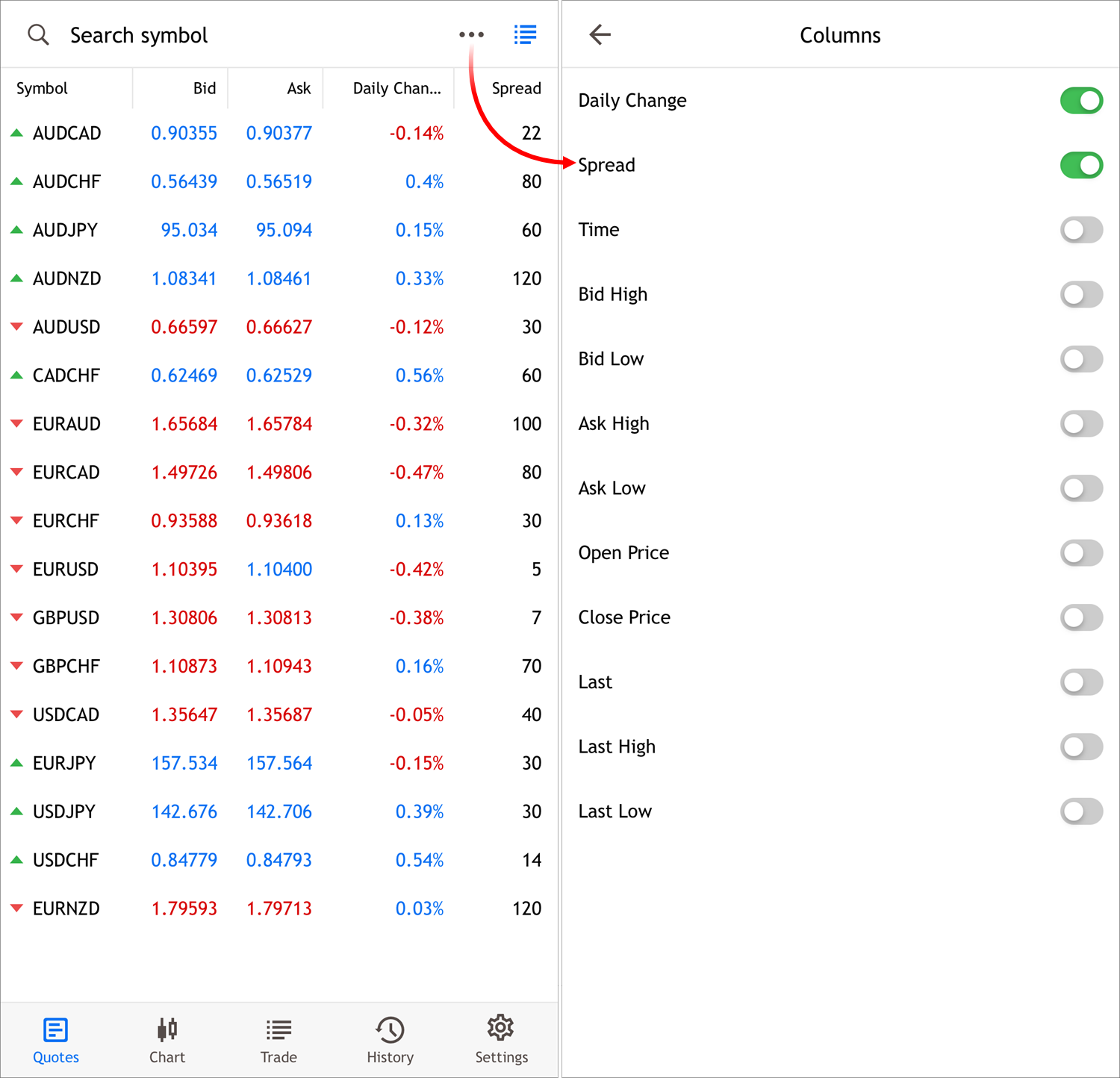
- Añadidas teclas de acceso rápido:
- Home — desplazamiento hasta el principio del gráfico (la fecha más antigua)
- End — desplazamiento hasta el final del gráfico (la fecha más reciente)
- Page Up — desplazamiento del gráfico una pantalla hacia atrás
- Page Down — desplazamiento del gráfico una pantalla hacia delante
- Se ha reforzado la seguridad del almacenamiento de datos de conexión de cuentas.
- Mejorado el desplazamiento, el movimiento y el zoom de los gráficos.
- Acelerada la carga inicial de la plataforma web en una página.
- Optimizada la carga de barras.
- Corregido el cálculo fijo del beneficio flotante para posiciones en instrumentos con el tipo Exchange Bonds y Exchange MOEX Bonds.
- Corregida la introducción del volumen en el panel de comercio rápido del gráfico.
- Corregido el error de actualización de los volúmenes de las órdenes en la profundidad de mercado. En algunos casos, los valores podían actualizarse con retraso.
- Corregida la comprobación fija del volumen mínimo admisible de una operación comercial al colocar órdenes.
- Corregido el cálculo del margen para las posiciones cubiertas. El error podría producirse en algunos casos cuando se utilizaba margen flotante en la cuenta (dependiendo del volumen/valor de las posiciones en la cuenta).
- Corregido el error que podía provocar que los botones Buy y Sell del panel de comercio rápido estuvieran inactivos antes de los cambios de volumen.
Terminal
- Corregido el bloqueo del terminal que se producía en algunos casos al ejecutar la simulación.
MQL5
- Corregido el funcionamiento de la propiedad MQL_PROGRAM_NAME para los programas de servicio. Antes, podía devolver un nombre no válido de ejemplar de servicio.
Web Terminal
- Corregida la comprobación de la compatibilidad del navegador con el terminal web. En algunos casos, los usuarios podían recibir un mensaje erróneo que informaba de la incompatibilidad de su navegador.
- Corregida la apertura de cuentas demo.
- Correcciones menores y mejoras.
La actualización estará disponible a través del sistema Live Update.
MetaTrader 5 Android
- Interfaz
completamente actualizada para la versión de la aplicación para
tabletas. Ahora usa un diseño moderno ya probado en las versiones iOS y
web de la plataforma. Las secciones principales se encuentran ahora en
la parte inferior de la pantalla, mientras que los comandos para
trabajar con el gráfico se encuentran en la parte izquierda de la
pantalla.

- Añadido un menú contextual en la sección de historia de posiciones que permite saltar rápidamente a la ventana de diálogo de operaciones o al gráfico del símbolo correspondiente.
- El comando para cambiar a la ventana de diálogo de comercio para los símbolos que no comercian está oculto.
- Corregido el trabajo con el servidor MetaQuotes-Demo.
Actualice sus aplicaciones móviles al build 4360 a través de Google Play, Huawei AppGallery o descargue el archivo APK.
Terminal
- Corregidos los errores que, en algunos casos, provocaban el mal funcionamiento del sistema Live Update.
- Añadida la tecla Alt+X para llamar a la lista de expertos.
- Correcciones de crash logs.
MetaTester
- Corregidos errores en la configuración de algunas propiedades del objeto gráfico "Imagen".
- MetaTester: Prohibido conectar agentes de prueba a la red MQL5 Cloud Network al trabajar en entornos virtuales y cuando el procesador no admite el conjunto de instrucciones AVX.
Terminal web
- Corregido un error en el panel de operaciones rápidas del gráfico.
- Corregido el cuadro de diálogo de advertencia que se abre al activar el panel de operaciones rápidas en un gráfico.
MetaEditor
- Añadida una página de inicio para ayudarle a comenzar su andadura en el trading algorítmico y el desarrollo de aplicaciones comerciales.
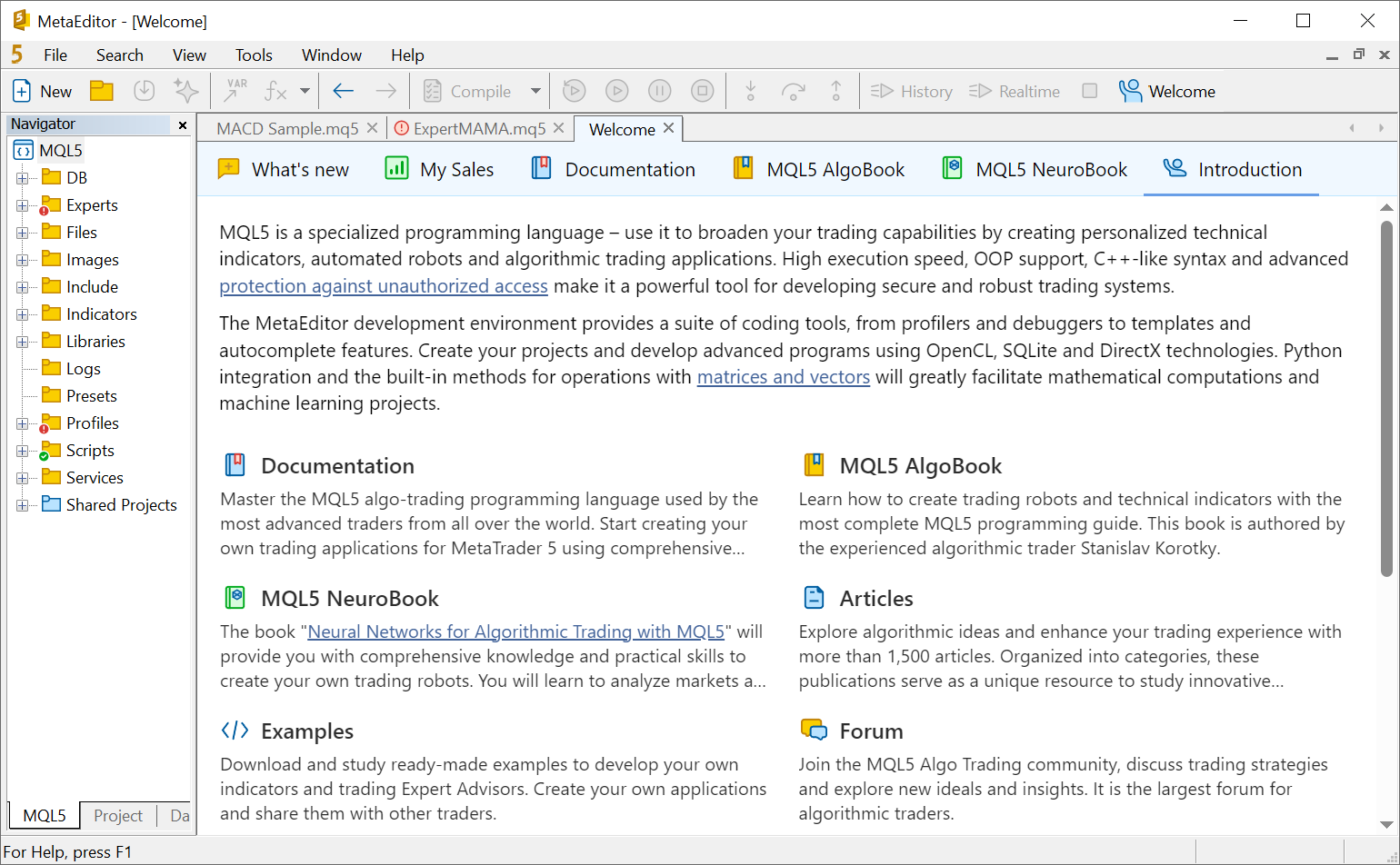
Materiales para principiantes
El apartado "Introducción" le informará detalladamente sobre los materiales de formación disponibles en MQL5.com: documentación completa sobre el lenguaje, libros, artículos y foro de desarrolladores, así como una biblioteca de códigos listos para usar. Aquí también se familiarizará con los servicios en los que podrá aplicar y monetizar sus conocimientos: el mercado de aplicaciones, la bolsa Freelance y las señales comerciales.
Consulte las secciones de la documentación y los libros para obtener una descripción más detallada de los tutoriales disponibles.
Funciones útiles para quienes se dedican al desarrollo
En la sección "Novedades", hemos recopilado toda la información que necesita un desarrollador para mantenerse al día:
- Los temas recientes en el foro de tráders y desarrolladores
- Los nuevos encargos en la bolsa Freelance
- Los últimos artículos sobre el desarrollo de aplicaciones
- Las publicaciones recientes en la biblioteca de código fuente
También verá una lista con los últimos archivos abiertos para el acceso rápido.
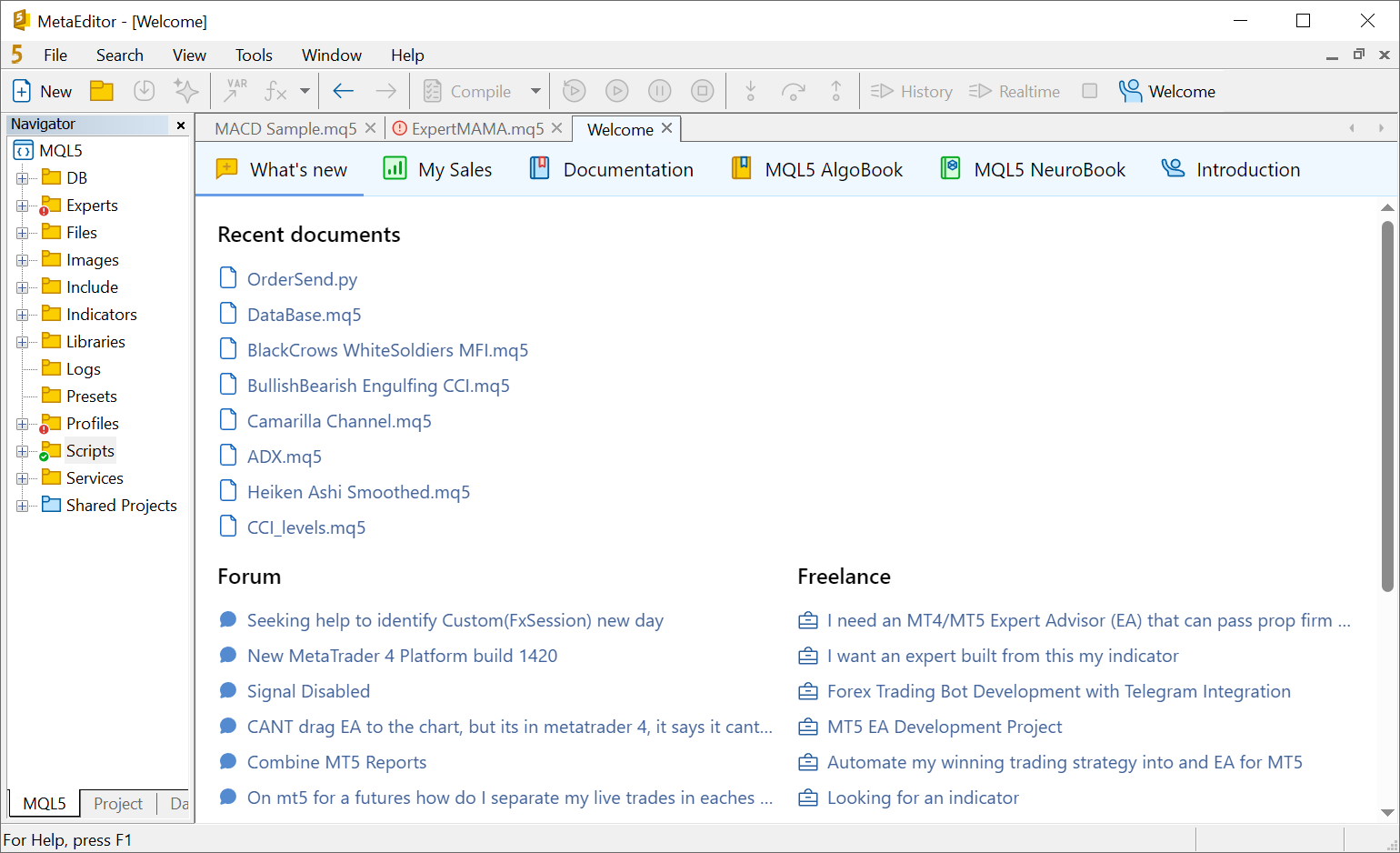
Si ya está vendiendo activamente sus aplicaciones en el Mercado, el informe "Mis ventas" le ayudará a evaluar sus progresos. Tendrá a su disposición:
- Las estadísticas de ventas totales y descargas por tiempo.
- La geografía de ventas para saber dónde son más populares sus desarrollos. Esto podrá sugerirle ideas para el desarrollo posterior del proyecto, por ejemplo, la localización a determinados idiomas o el lanzamiento de publicidad en una región determinada.
- Los datos sobre los productos más populares por número de ventas e importe de los ingresos. El calendario puede filtrarse por tipo de licencia: licencia completa o alquiler de una duración determinada. Aquí tendrá también un gráfico con la evolución del precio del producto. Todo ello le ayudará a comprender mejor a sus clientes.
- Estadísticas detalladas de descargas y ventas de cada producto.
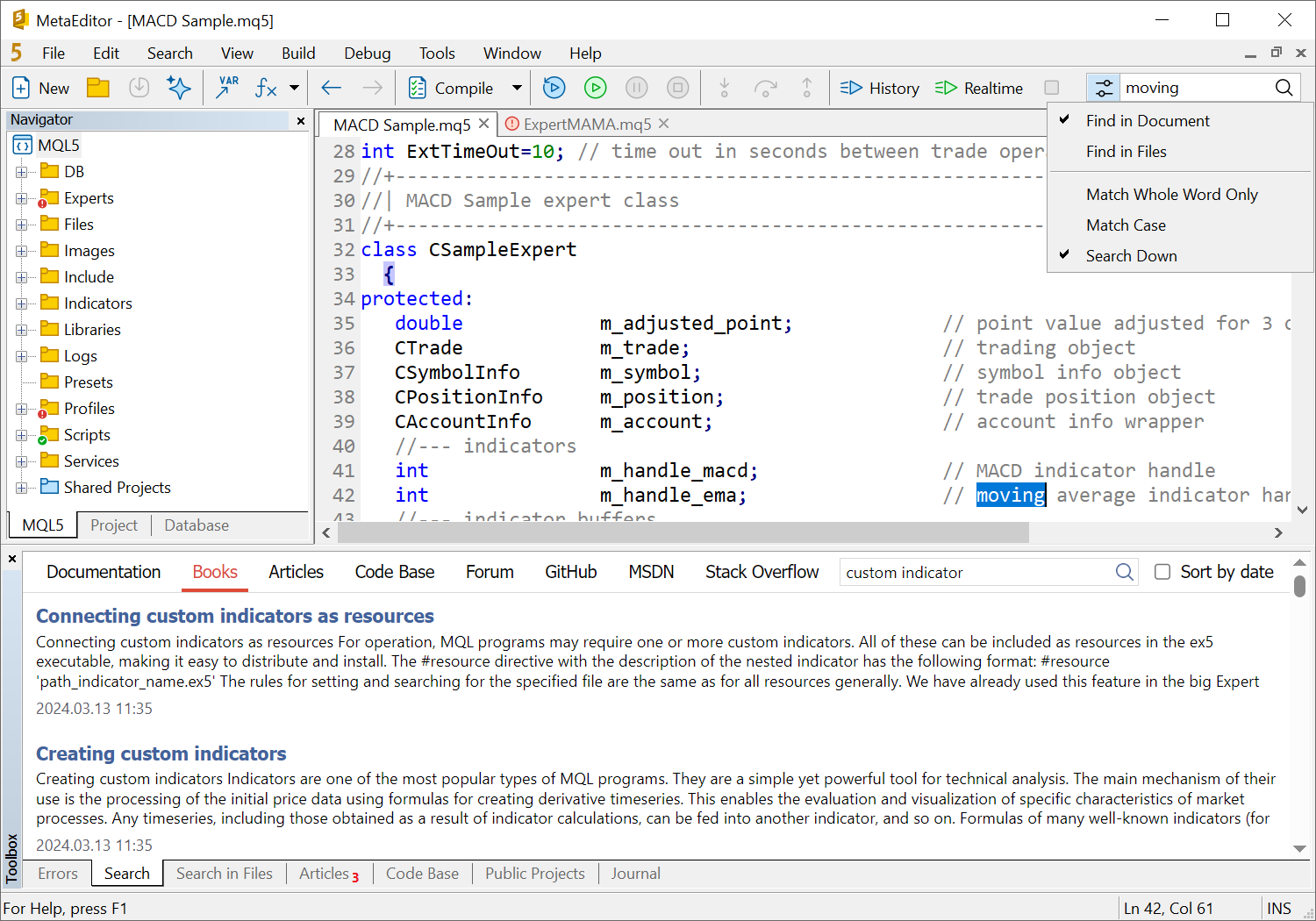
- Mejorada la búsqueda incorporada. La barra de búsqueda superior ahora solo se utilizará para buscar texto en el documento actual o en archivos locales. Utilice la sección aparte en "Herramientas" para buscar tutoriales y códigos de forma global.
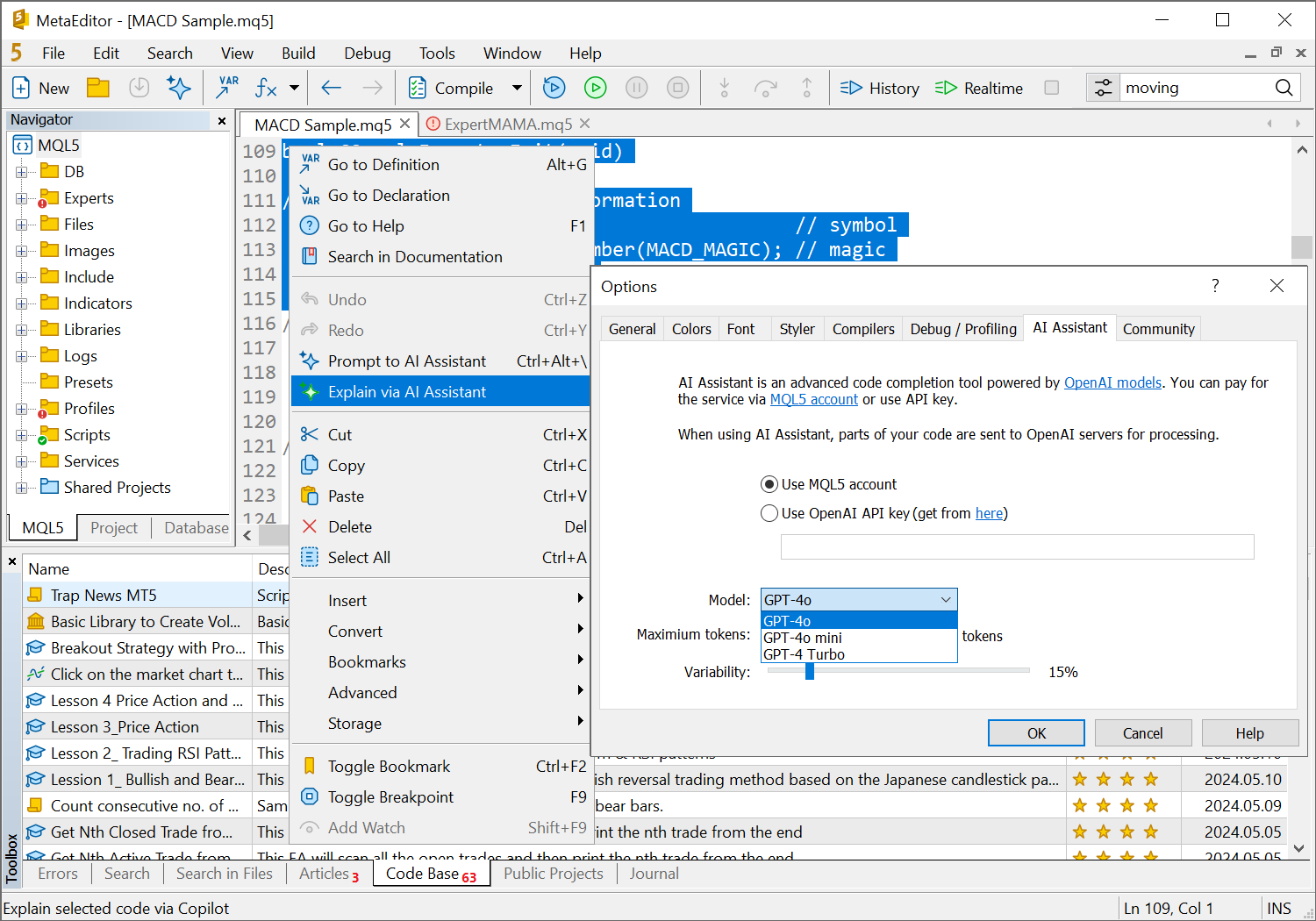
- Añadida la compatibilidad con GPT-4o, el último modelo de ChatGPT, para AI Assistant. Ahora podrá utilizarlo para completar automáticamente el código y obtener pistas. Podrá seleccionar un nuevo modelo en los ajustes del MetaEditor.
- Actualizadas las traducciones de la interfaz de usuario.
Terminal
- Mayor precisión de la visualización del precio calculado en las especificaciones del instrumento comercial.
- Corregido el cálculo de los indicadores MFE y MAE en el informe comercial.
- Corregido el guardado y restablecimiento de los ajustes de filtrado del calendario económico por país y divisa.
- Corregida la aplicación de plantillas a los gráficos. Ahora, si la visualización de la historia comercial está activada para un gráfico, los objetos correspondientes no desaparecerán después de aplicar la plantilla.
- Corregido un error en el funcionamiento del panel de opciones. En algunos casos, la plataforma podía bloquearse al añadir símbolos.
- Corregido un error en la ventana de diálogo de edición de posiciones. En algunos casos, en lugar de los valores actuales de Stop Loss y Take Profit, los campos correspondientes podían sustituirse por valores incorrectos.
- Actualizadas las traducciones de la interfaz de usuario.
MQL5
- La función ArrayResize se ha optimizado y acelerado considerablemente. En algunos casos, la aceleración puede llegar al 40%.
- Actualizada la compatibilidad con ONNX.
- Corregida la llamada a la función MessageBox en los programas de servicio. Independientemente del botón que pulsara el usuario en la ventana de diálogo, la función retornaba un valor nulo.
- Corregido el error que, en algunos casos, provocaba una inicialización incompleta de los programas MQL5.
- Corregido el error de análisis de algunas macros. El error se producía al utilizar un gran número de constantes.
Terminal web MetaTrader 5
- Ampliado el conjunto de objetos analíticos disponibles. Ahora podrá utilizar una "regla" para medir el tiempo y los precios, las figuras (rectángulo, elipse, triángulo, círculo) y añadir cualquier rótulo al gráfico. Todos los objetos estarán disponibles en el panel izquierdo:
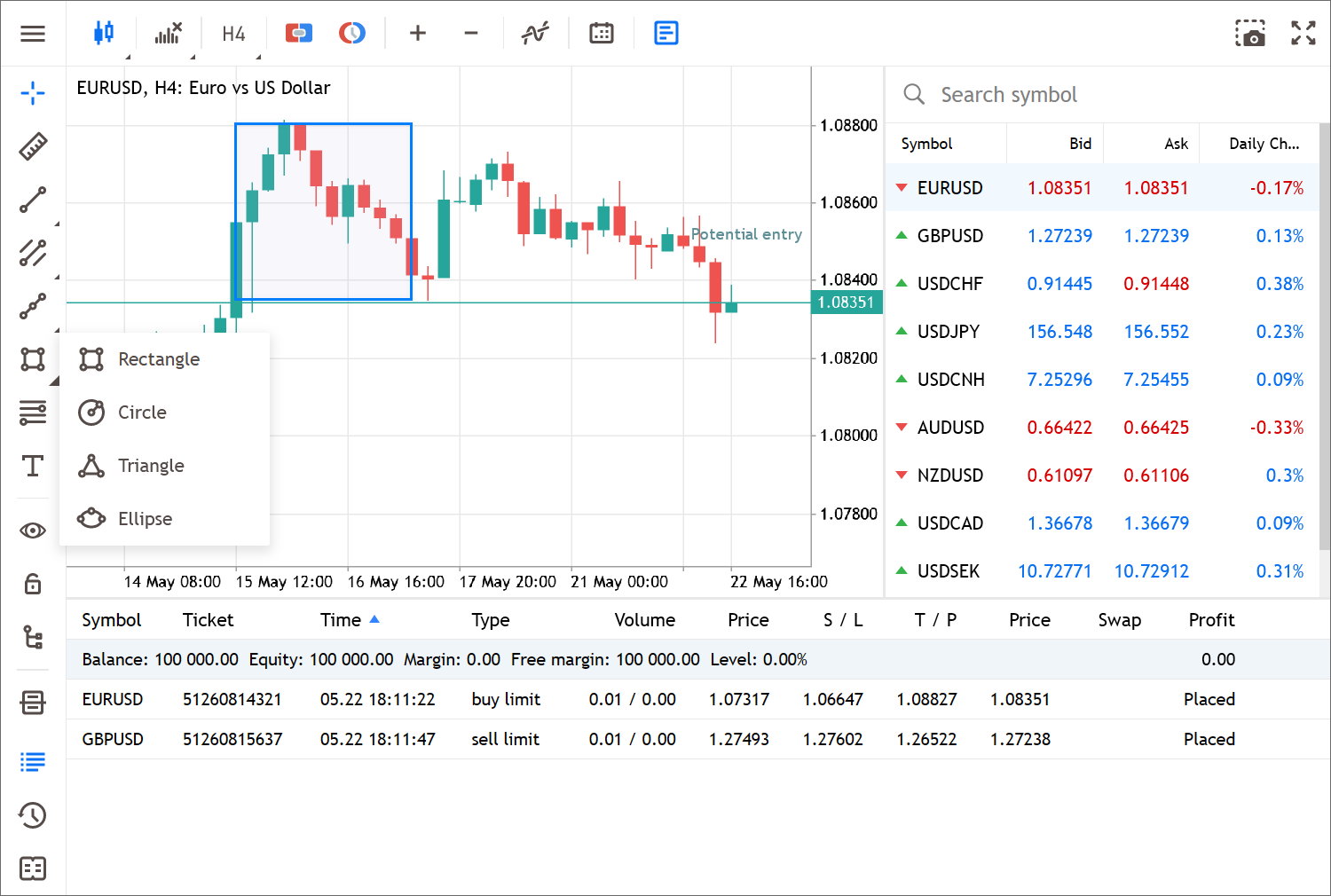
- Añadida la posibilidad de renombrar objetos.
- Mayor integración con el calendario económico. Optimizada y acelerada la consulta de datos.
- Acelerado el funcionamiento de los gráficos.
- Acelerados el inicio de la aplicación y la conexión a la cuenta comercial.
- Corregido el funcionamiento del ajuste que controla la visualización de las operaciones comerciales en el gráfico.
- Corregida la visualización de los requisitos de margen en las especificaciones del contrato.
- Corregida la visualización del estado de la cuenta en la sección de la historia. El problema se producía en dispositivos con una pantalla estrecha.
- Corregida la visualización de la profundidad de mercado.
Terminal
- Corregido el error al suscribirse a productos gratuitos en el servicio “Suscripciones”. En algunos casos, es posible que el botón correspondiente no esté presente en la ventana de diálogo.
- Actualizadas las traducciones de la interfaz de usuario.
MQL5
- Ampliado el soporte para eventos de teclado:
- Añadido el evento CHARTEVENT_KEYUP al manejador OnChartEvent. Dicho evento permite monitorear el momento en que el usuario suelta una tecla en el teclado.
- Añadido el procesamiento de teclas "muertas" (Dead keys), es decir, las teclas que permiten cambiar el tipo del siguiente carácter introducido. Por ejemplo, en la composición griega, poner énfasis en las vocales ά, έ, ύ, etc., debemos presionar la tecla “;” y luego introducir una letra. Ahora la pulsación de dichas teclas se puede monitorear utilizando la función TranslateKey.
- Mejoradas las funciones TranslateKey y TerminalInfoInteger. Ahora, al recibir eventos CHARTEVENT_KEYUP o CHARTEVENT_KEYDOWN en OnChartEvent, podremos obtener el estado completo del teclado en el momento en que ha ocurrido el evento. Por ejemplo, si el usuario ha presionado la tecla Z, podrá saber si en ese momento se ha presionado la tecla Ctrl o Shift. Para otros eventos, las funciones operarán como antes: retornarán el estado del teclado en el momento actual.
-
Actualizada la biblioteca Alglib. Debido a la actualización, se han
cambiado los siguientes métodos en las clases CMatrixDouble y
CMatrixComplex:
vector<double/complex> operator[](const int i) const; vector<double/complex> operator[](const ulong i) const;
Ahora, en lugar de ellos, se utilizará un método con un valor de retorno constante:
const vector<double/complex> operator[](const ulong i) const;
La corrección realizada nos permitirá detectar el uso incorrecto del resultado: en la nueva versión de Alglib, el código mat[row][col]=x funciona de forma diferente que en la anterior. Antes, esto suponía la escritura en un array, pero ahora supone la escritura en un objeto vectorial temporal <double/complex> que se destruye inmediatamente después de la escritura.
La adición de const al valor retornado hace que resulte imposible usar mat[row][col]=x. Debido a que mat[row] ahora retorna un vector constante, intentar sobrescribir su elemento con mat[row][col] provocará un error de compilación.
- Corregido el error que en algunos casos provocaba un funcionamiento incorrecto de las funciones ChartGet*.
MetaEditor
- Añadida la búsqueda en el libro “Redes neuronales en el trading algorítmico en MQL5”. Ahora se combina en una sección con el libro publicado anteriormente "Programación en MQL5 para tráders".

Tester
- Corregida la optimización para una gran cantidad de agentes remotos. En algunos casos, el error podría provocar una carga excesiva de la CPU.
Terminal web MetaTrader 5
- Corregida la colocación de órdenes límite para instrumentos con ejecución bursátil. Ahora, cuando el precio de la orden colocada cambia en relación con el actual (más alto o más bajo), el tipo de orden propuesta no cambiará de Buy Limit a Sell Limit y viceversa, como ocurre con otros tipos de instrumentos. Así, el usuario, si es necesario, podrá colocar órdenes Buy Limit por encima del mercado y órdenes Sell Limit por debajo del mercado para limitar el precio de la transacción de forma garantizada.
- Corregida la visualización de contadores para los símbolos seleccionados en la «Observación de mercado».
Terminal
-
Añadidos 28 asesores y 12 indicadores nuevos al paquete estándar de la
plataforma. Las aplicaciones estarán disponibles en las secciones
“Asesores\Free Robots" e “Indicadores\Free Indicators" del Navegador.
Para cada uno de ellos está disponible el código fuente con comentarios
detallados que le ayudarán a aprender el lenguaje MQL5.
Los robots implementan estrategias comerciales basadas en indicadores técnicos y patrones de velas, como 3 Black Crows – 3 White Soldiers, Bullish Engulfing – Bearish Engulfing, Bullish Harami – Bearish Harami y otros. Los nuevos indicadores suponen la implementación de canales populares: Camarilla, DeMark, Donchian, Fibonacci, Keltner y otros.
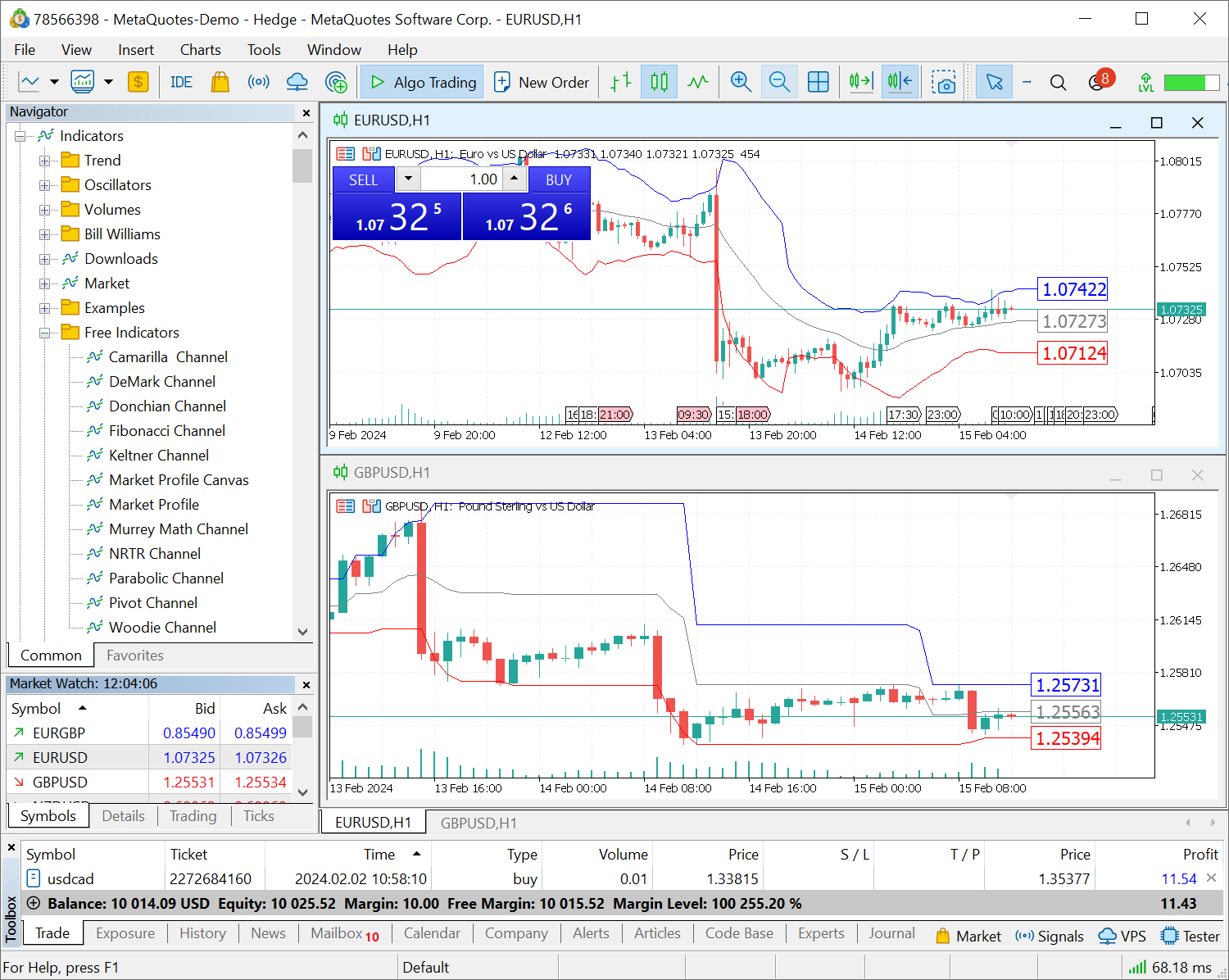
- Estamos realizando los preparativos necesarios para lanzar suscripciones a los datos del mercado Nasdaq.
Directamente desde la plataforma, los tráders podrán acceder a las
cotizaciones en tiempo real y la historia de precios detallada de
cientos de instrumentos financieros de una de las mayores bolsas del
mundo. Para hacer esto, solo necesitará una cuenta demo en el servidor
MetaQuotes-Demo y una cuenta en MQL5.community.
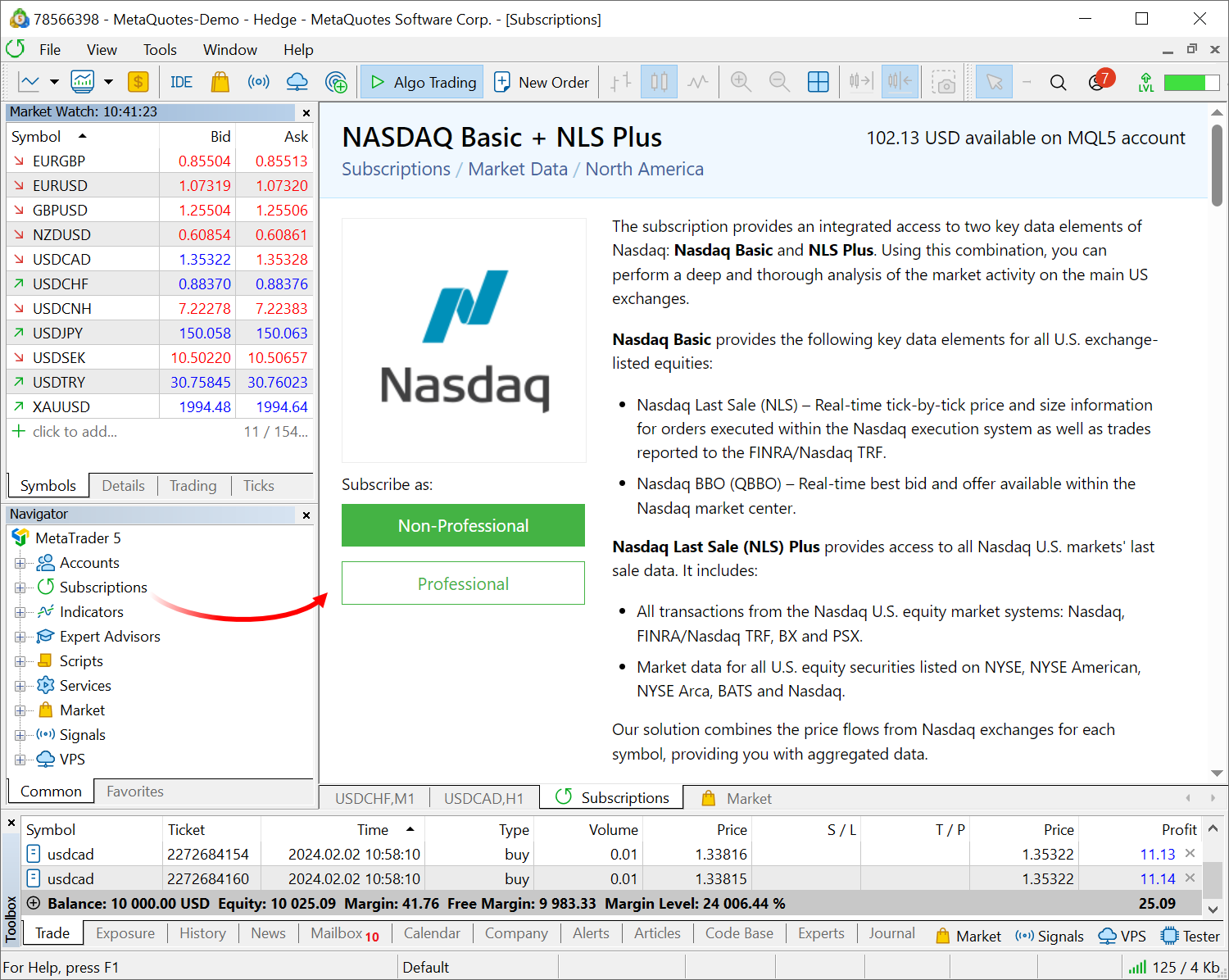
Una vez se haya suscrito, simplemente añada los instrumentos correspondientes a su Observación de Mercado y comience a trabajar. Podrá abrir gráficos de estos, analizarlos utilizando cualquier objeto e indicador y también usar los datos para probar estrategias comerciales en el simulador. El acceso a toda la información se realizará de la forma habitual: como en los instrumentos financieros ordinarios con los que usted trabaja con el bróker. - Mejorada la
sección de margen en las especificaciones del instrumento. Ahora
mostrará tanto los coeficientes de margen para cada tipo de instrumento
como los valores finales de margen calculados.
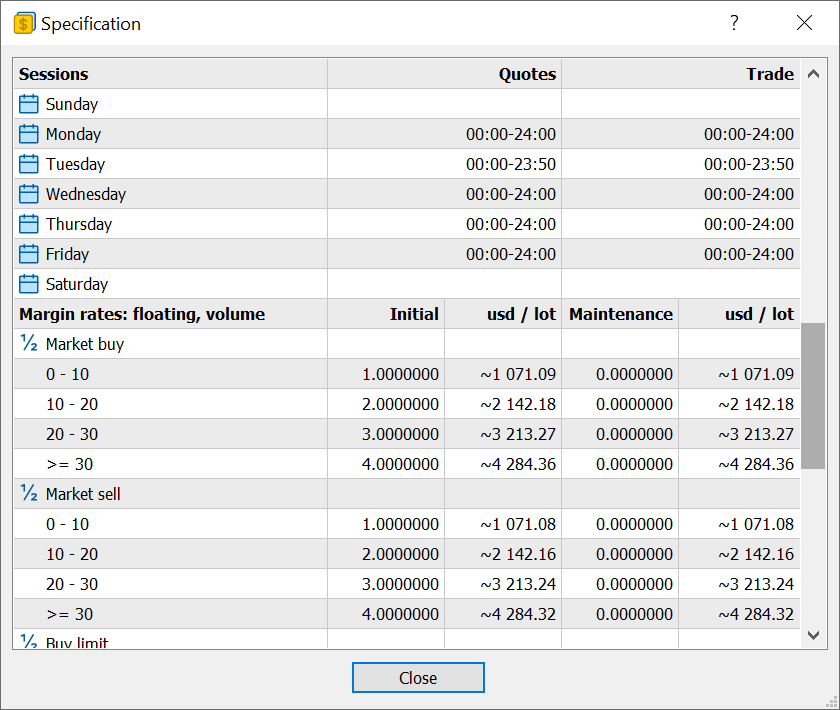
También se han solucionado algunos errores en la representación de los márgenes para algunos tipos de instrumentos.
- Añadido un enlace al canal MQL5 Telegram en el menú "Ayuda". El canal publica periódicamente materiales interesantes para desarrolladores: reseñas de nuevos artículos sobre programación y robots e indicadores gratuitos de la biblioteca de códigos. Suscríbase al canal para no perderse información importante.
- Añadido soporte para el parámetro ShutdownTerminal en la sección [StartUp] de los archivos de configuración del usuario. Use esta opción para iniciar la plataforma y realizar tareas únicas mediante scripts. Por ejemplo, dispondrá de un script que toma una captura de pantalla de un gráfico. Podrá crear un archivo de configuración que ejecutará este script junto con la plataforma. Si le añade ShutdownTerminal con el valor "Yes", la plataforma se cerrará automáticamente justo después de que se complete el script.
- Reforzada la protección de los protocolos y productos de red en el Mercado.
- Desactivada la compatibilidad con el servicio "Señales" para cuentas demo. Para obtener estadísticas avanzadas sobre sus cuentas de entrenamiento, utilice el nuevo informe comercial. Este ofrece un gran número de métricas sobre la rentabilidad y el riesgo de su estrategia, contiene gráficos de crecimiento, balance y equidad, gráficos de distribución de transacciones por dirección e instrumentos, y mucho más.
- Corregida la representación de enlaces a los acuerdos de brókeres en el menú “Ayuda".
- Mejorada la selección del mejor servidor al alquilar un VPS.
- Corregida la actualización de la página de suscripciones al cambiar de sección en el navegador.
- Corregida la actualización de la lista de acuerdos al abrir una cuenta preliminar.
- Actualizadas las traducciones de la interfaz de usuario.
MQL5
- Añadida la propiedad MQL_STARTED_FROM_CONFIG a la enumeración ENUM_MQL_INFO_INTEGER. Esta retornará true si el script/experto se ha iniciado desde la sección StartUp del archivo de configuración.
Esto significará que dicho script/experto ha sido registrado en el
archivo de configuración con el que se ha iniciado el terminal.
- Continúan los trabajos de ampliación del soporte para los modelos ONNX.
Las tareas de aprendizaje automático no siempre requieren una mayor precisión computacional. Para acelerar los cálculos, algunos modelos usan tipos de datos con menor precisión, como Float16 e incluso Float8. Para permitir a los usuarios suministrar dichos datos a la entrada del modelo, hemos añadido las siguientes funciones a MQL5:
bool ArrayToFP16(ushort &dst_array[],const float &src_array[],ENUM_FLOAT16_FORMAT fmt); bool ArrayToFP16(ushort &dst_array[],const double &src_array[],ENUM_FLOAT16_FORMAT fmt); bool ArrayToFP8(uchar &dst_array[],const float &src_array[],ENUM_FLOAT8_FORMAT fmt); bool ArrayToFP8(uchar &dst_array[],const double &src_array[],ENUM_FLOAT8_FORMAT fmt); bool ArrayFromFP16(float &dst_array[],const ushort &src_array[],ENUM_FLOAT16_FORMAT fmt); bool ArrayFromFP16(double &dst_array[],const ushort &src_array[],ENUM_FLOAT16_FORMAT fmt); bool ArrayFromFP8(float &dst_array[],const uchar &src_array[],ENUM_FLOAT8_FORMAT fmt); bool ArrayFromFP8(double &dst_array[],const uchar &src_array[],ENUM_FLOAT8_FORMAT fmt);
Como los formatos de números reales para 16 y 8 bits pueden diferir, en el parámetro fmt en las funciones de conversión se deberá indicar qué formato de número debe procesarse. Para las versiones de 16 bits se utilizará la nueva enumeración NUM_FLOAT16_FORMAT, que actualmente tiene los siguientes valores:
- FLOAT_FP16 es un formato estándar de 16 bits, también conocido como half.
- FLOAT_BFP16 es el formato especial brain float point.
Para las versiones de 8 bits, se utilizará una nueva enumeración, ENUM_FLOAT8_FORMAT, que actualmente tiene los siguientes valores:
- FLOAT_FP8_E4M3FN
es un número de punto flotante de 8 bits, 4 bits de exponente y 3 bits
de mantisa. Normalmente se usa como coeficientes.
- FLOAT_FP8_E4M3FNUZ es un número de coma flotante de 8 bits, 4 bits de exponente y 3 bits de mantisa. Admite NaN; no admite cero negativo e Inf. Normalmente se usa como coeficientes.
- FLOAT_FP8_E5M2FN es un número de coma
flotante de 8 bits, 5 bits de exponente y 2 bits de mantisa. Ofrece
soporte a NaN e Inf. Normalmente se utiliza para gradientes.
- FLOAT_FP8_E5M2FNUZ
es un número de coma flotante de 8 bits, 5 bits de exponente y 2 bits
de mantisa. Admite NaN e Inf, no admite cero negativo. También se
utiliza para gradientes.
- FLOAT_FP16 es un formato estándar de 16 bits, también conocido como half.
- Añadidos nuevos métodos matriciales y vectoriales utilizados en el aprendizaje automático:
- PrecisionRecall — calcula los valores para crear la curva precision-recall. Este método, al igual que el método ClassificationScore, se aplica a un vector de valores verdaderos.
- ReceiverOperatingCharacteristic — calcula los valores para trazar la curva Receiver Operating Characteristic (ROC). Este método, al igual que el método ClassificationScore, se aplicará a un vector de valores verdaderos.
- ONNX Runtime se ha actualizado a la versión 1.17. Los detalles de la versión están disponibles en GitHub.
- El paquete de integración de Python
se actualizado a la versión 5.0.4200, añadiendo soporte para Python
3.12. Actualice su paquete con "pip install --upgrade MetaTrader5" para
obtener los últimos cambios.
- Corregido el funcionamiento de la función OrderCalcMargin para algunos casos.
- Añadido el valor DEAL_REASON_CORPORATE_ACTION a la enumeración ENUM_DEAL_REASON: la transacción se ha realizado como resultado de una acción corporativa: fusión o cambio de nombre de un valor, traspaso de un cliente a otra cuenta, etc.
- Añadido soporte para comparar vectores complejos y matrices para el método Compare. La comparación consistirá en estimar la distancia entre números complejos. La distancia se calculará usando la siguiente fórmula sqrt(pow(r1-r2, 2) + pow(i1-i2, 2)) y será un número real que ya podrá compararse con épsilon.
- Corregida la conversión de variables de tipo color a texto en formato RGB.
- Corregido el retorno del resultado de la obtención de vectores propios en el método Eig en caso de valor propio complejo. Añadida sobrecarga de métodos para una solución compleja.
MetaEditor
- Añadido un enlace al libro recientemente publicado “Programación MQL5 para tráders”
en el menú Ayuda\MQL5.community. El libro también ha sido añadido al
sistema de búsqueda, podrá encontrar los materiales necesarios en él
directamente desde el MetaEditor:
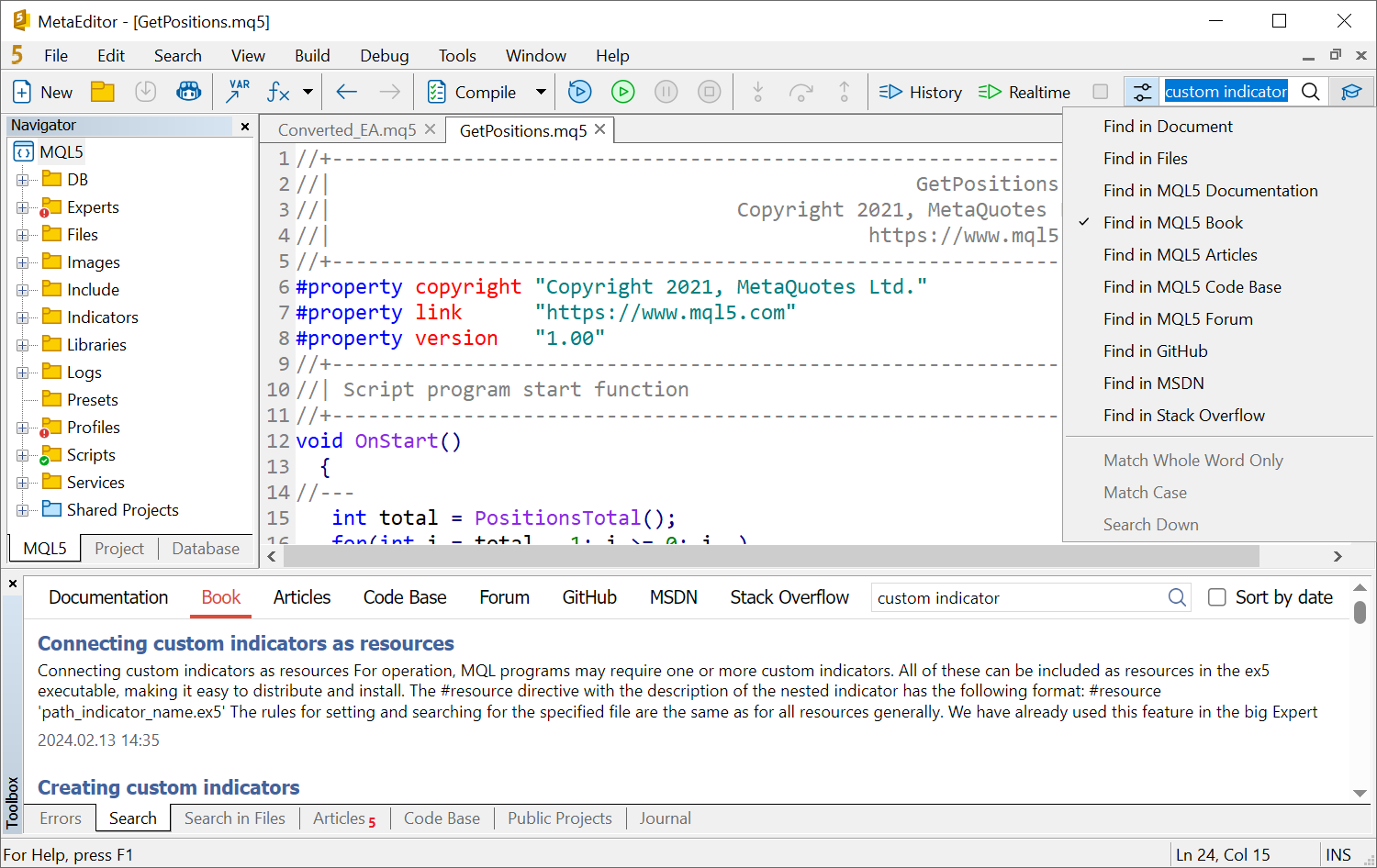
- Mejorada la búsqueda integrada:
- La sección de resultados de búsqueda de la ventana "Herramientas" está dividida en dos pestañas: "Buscar" – para los resultados de búsqueda en línea (documentación, artículos, libros, etc.), “Buscar en archivos” – para los resultados locales.
- Se ha añadido una barra de
búsqueda aparte a la sección de resultados. Podrá usarla en lugar de la
barra de búsqueda en el panel de herramientas principal del MetaEditor.
- Añadido soporte para los modos AVX, AVX2 y AVX512 al compilar programas desde la línea de comandos. Para hacer esto, añada una de las claves al comando: /avx, /avx2 o /avx512.
- El motor SQLite para trabajar con bases de datos se ha actualizado a la versión 3.45.
- Deshabilitada la compatibilidad con Internet Explorer. Ahora solo se utilizará Microsoft Edge WebView2 para mostrar páginas HTML. En comparación con el MSHTML heredado, el nuevo componente expandirá significativamente las capacidades para mostrar contenido web, proporcionando acceso a tecnologías modernas. El cambio a WebView2 mejorará la apariencia de algunas secciones del MetaEditor, aumentará su rendimiento y creará interfaces más receptivas.
- Corregido el bloqueo que sucedía en raras ocasiones al completar automáticamente funciones.
- Corregido el bloqueo que sucedía en raras ocasiones al completar automáticamente funciones.
Simulador
- Corregido el cálculo del swap triple en caso de que el día de inicio de la prueba caiga en un día de swap triple.
Correcciones de crash logs.
MetaTrader 5 Web Terminal
Mejorada
la representación de los requisitos de margen en las especificaciones
del contrato. Ahora, además de los coeficientes y parámetros iniciales
para el cálculo, se mostrará el valor final del margen. Si el monto del
margen depende del volumen de la posición, los niveles correspondientes
se mostrarán en la ventana de diálogo.
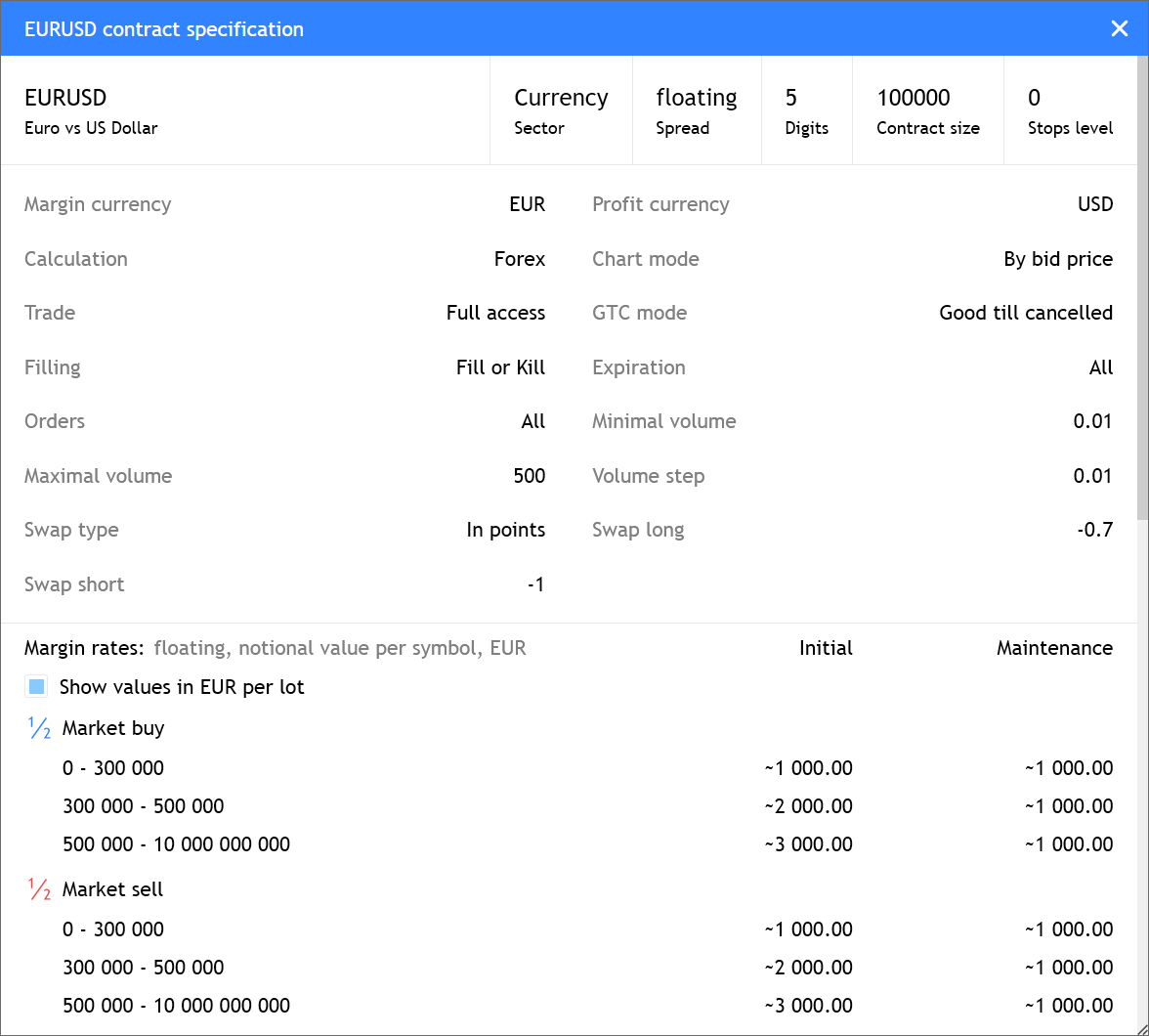
El margen se calcula considerando el precio del instrumento en el momento en que se abre la ventana de especificaciones y no cambia en tiempo real. En consecuencia, los valores deberán tomarse únicamente como indicativos. Para volver a calcular los valores a los precios actuales, abra nuevamente la especificaciones del instrumento.
Terminal
- Añadida la exportación del informe comercial a un archivo HTML y PDF. Ahora podrá compartir fácilmente sus logros
comerciales con colegas o inversores. Para realizar la exportación,
utilice el menú en el propio informe o en el menú «Archivo».
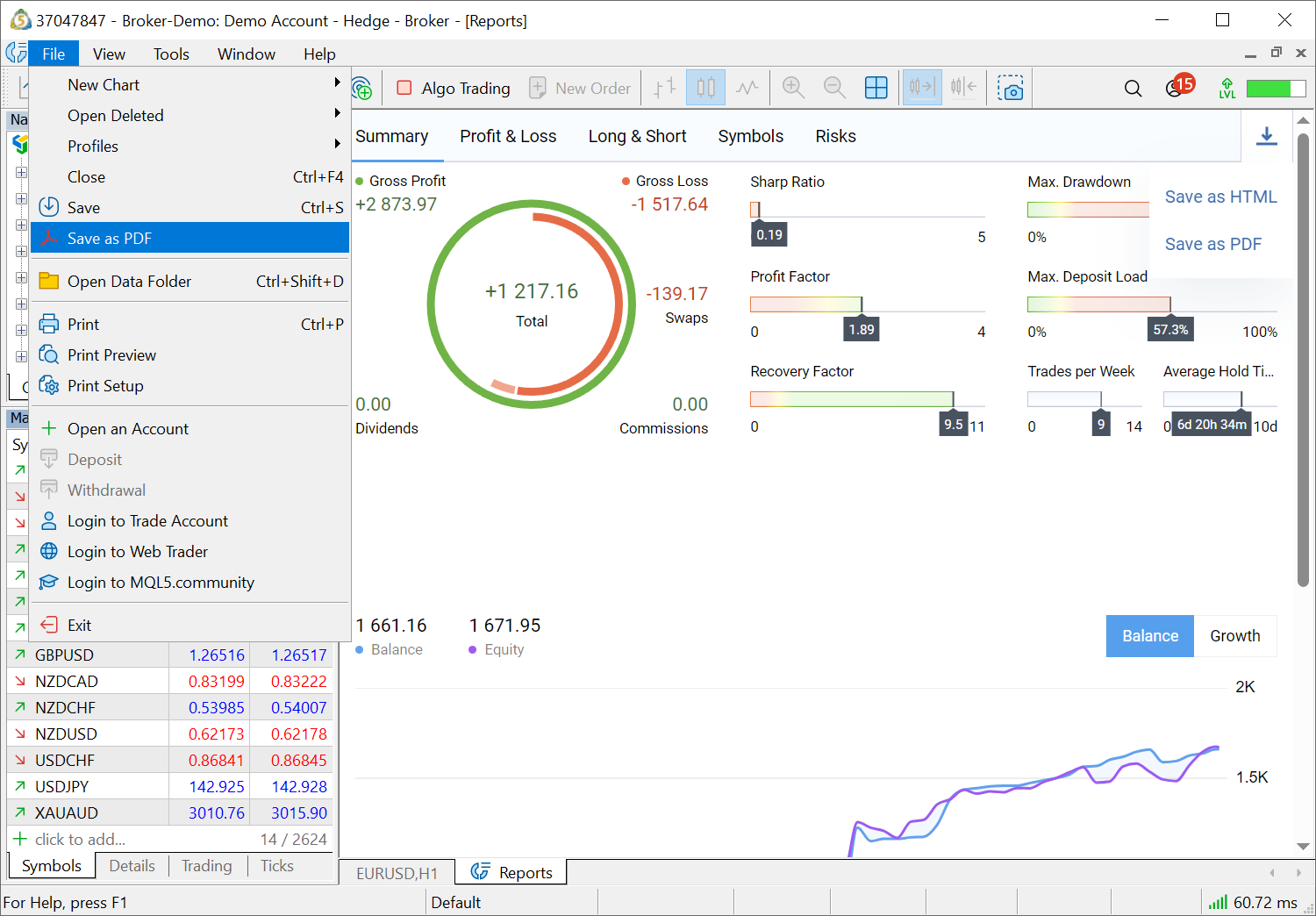
- Añadida la capacidad de guardar el estado actual de la ventana de «Observación de mercado»
en un archivo CSV. Para hacer esto, clique en "Exportar" en el menú
contextual. El archivo guardará los valores de los indicadores
seleccionados al momento de la exportación. Para descargar más datos,
active columnas adicionales a través del menú contextual.
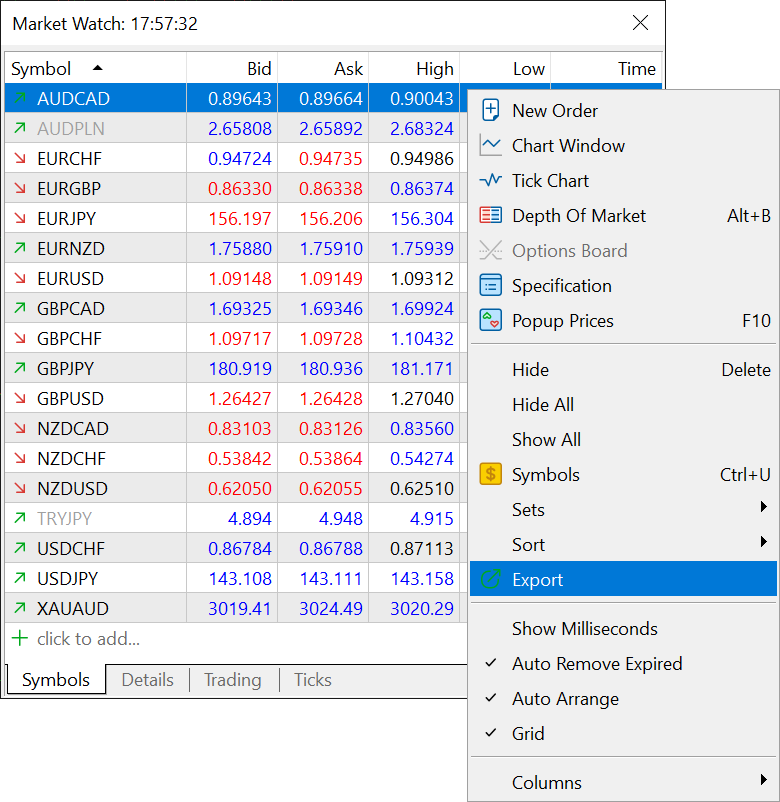
- Visualización mejorada de los requisitos de margen en las
especificaciones del contrato. Ahora, en lugar de los coeficientes y
parámetros iniciales para el cálculo, se mostrará el valor final del
margen. Si el monto del margen depende del volumen de la posición, los
niveles correspondientes se mostrarán en la ventana de diálogo.
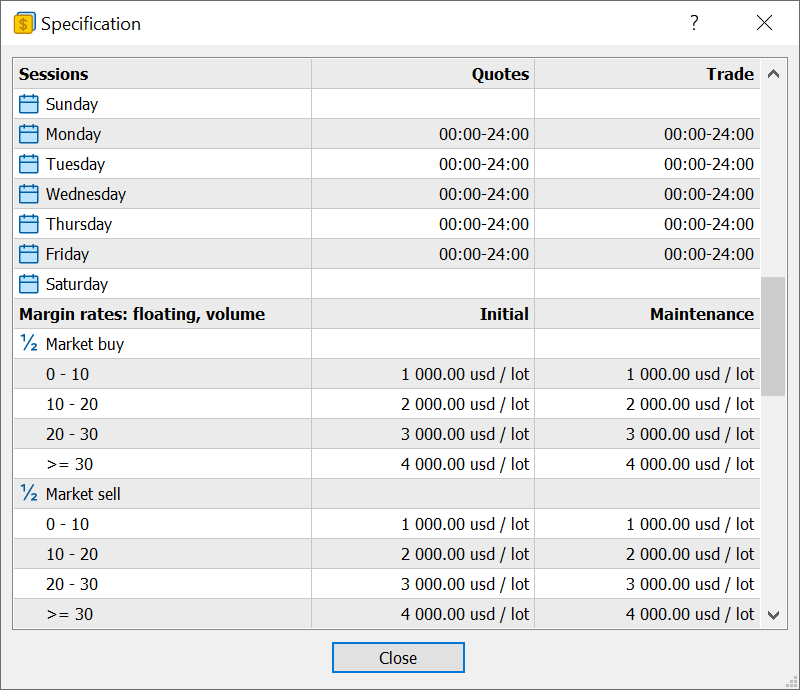
El margen se calcula considerando el precio del instrumento en el momento en que se abre la ventana de especificaciones y no cambia en tiempo real. En consecuencia, los valores deberán tomarse únicamente como indicativos. Para volver a calcular los valores a los precios actuales, abra nuevamente la especificaciones del instrumento.
- Desactivada la compatibilidad con el servicio "Señales" para cuentas demo. Para obtener estadísticas avanzadas sobre sus cuentas de entrenamiento, utilice el nuevo informe comercial.
Este ofrece una gran cantidad de indicadores sobre la rentabilidad y el
riesgo de su estrategia, así como gráficos de crecimiento, balance y
equidad, gráficos de distribución de transacciones por dirección e
instrumentos, y mucho más.
- Corregida la visualización de las ganancias/pérdidas potenciales al editar el Take Profit y el Stop Loss para las órdenes Stop Limit.
- Numerosas correcciones y mejoras en el sistema de pago.
- Corregida la verificación de duplicados al cargar un conjunto de herramientas en la "Observación de Mercado" desde un archivo *.set.
- Corregido el instalador web de Paralles. Ahora, al utilizar este
sistema de virtualización en macOS con procesadores M1/M2/M3, la
plataforma se instalará correctamente.
- Actualizadas las traducciones de la interfaz de usuario.
- Correcciones de crash logs.
MQL5
- MQL5: Añadidos nuevos métodos para trabajar con matrices y vectores. Se utilizan en el aprendizaje automático.
- ConfusionMatrix: calcula la matriz de error. El método se aplica al vector de valores predichos.
- ConfusionMatrixMultilabel: calcula la matriz de error para cada etiqueta. El método se aplica al vector de valores predichos.
- ClassificationMetric: calcula una métrica de clasificación para evaluar la calidad de los datos previstos en relación con los datos verdaderos. El método se aplica al vector de valores predichos.
- ClassificationScore:
calcula una métrica de clasificación para evaluar la calidad de los
datos pronosticados en relación con los datos verdaderos. El método se
aplica a un vector de valores verdaderos.
- Corregido el guardado de datos en un archivo de texto UTF-8 usando la función FileWrite.
- Desactivadas y declaradas como anticuadas las funciones Signal*. Ahora retornarán conjuntos de señales vacíos.
MetaEditor
- Aumentada la frecuencia de muestreo al realizar el perfilado. Ahora el estado de la aplicación se captura 10.000 veces por segundo, lo cual permite medir la velocidad de ejecución de la función con mucha más precisión.
- Actualizados los modelos disponibles en la herramienta de adición automática de código AI Assistant. Añadido el modelo ChatGPT-4 Turbo: se han eliminado las implementaciones obsoletas.
- Corregidos los errores al reemplazar palabras en un fragmento de texto seleccionado.
Simulador
- Corregido el bloqueo de las pruebas forward. El problema podía ocurrir en el modo de optimización genética.
- Optimizado y significativamente acelerado el trabajo con la historia comercial de los programas MQL5.
- Corregido el cálculo del beneficio en las operaciones de cierre con orden opuesta. El error podía ocurrir con instrumentos comerciales que no son la principal herramienta de prueba.
Terminal web
- Corregida la actualización de las propiedades de los instrumentos comerciales cuando estas se modifican por parte del bróker.
- Corregida la visualización del cuerpo de la vela en el gráfico. De ser pequeño, el cuerpo podía no resultar visible.
- Corregido el funcionamiento del campo “País” en el formulario de apertura de la cuenta.