MetaTrader 5 build 3390: Float in OpenCL and in mathematical functions, Activation and Loss methods for machine learning

Terminal

1. Added automatic opening of a tutorial during the first connection to a trading account. This will assist beginners in learning trading basics and in exploring platform features. The tutorial is divided into several sections, each of which provides brief information on a specific topic. The topic completion progress is shown with a blue line.
   

   
   

2. Fixed 'Close profitable'/'Close losing' bulk operations. Previously, the platform used opposite positions if they existed. For example, if you had two losing Buy positions for EURUSD and one profitable Sell position for EURUSD, all three positions would be closed during the 'Close losing' bulk operation. Buy and Sell would be closed by a 'Close by' operation, while the remaining Buy would be closed by a normal operation. Now the commands operate properly: they only close the selected positions, either profitable or losing.
   
3. Fixed display of negative historical prices. Such prices will appear correctly for all timeframes.
   
4. Optimized and significantly reduced system resource consumption by the terminal.
5. Updated fundamental database for trading instruments. The number of data aggregators available for exchange instruments has been expanded to 15. Users will be able to access information on even more tickers via the most popular economic aggregators.
   

   

   
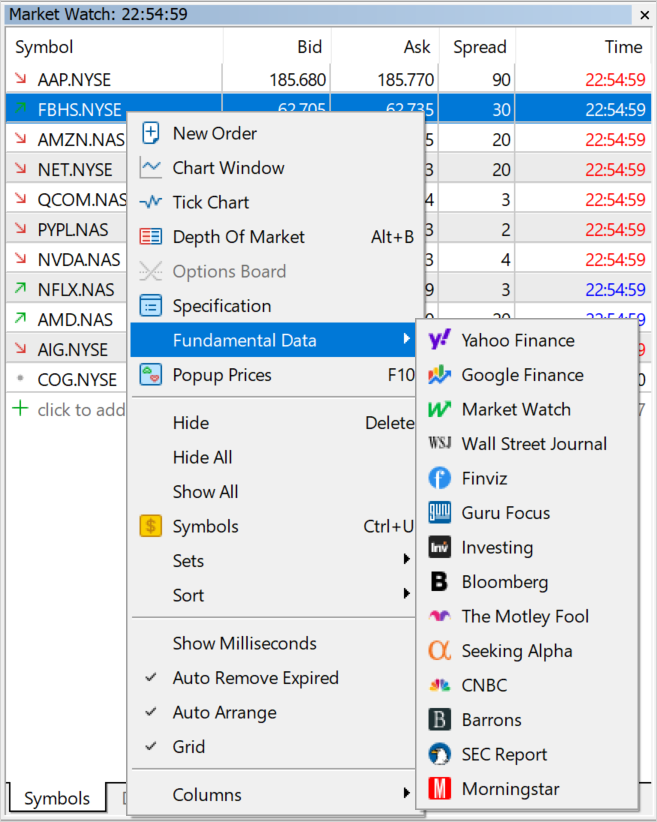
   About 7,000 securities and more than 2,000 ETFs are listed on the global exchange market. Furthermore, exchanges provide futures and other derivatives. The MetaTrader 5 platform offers access to a huge database of exchange instruments. To access the relevant fundamental data, users can switch to the selected aggregator's website in one click directly from the Market Watch. For convenience, the platform includes a selection of information sources for each financial instrument.
   
6. Fixed Stop Loss and Take Profit indication in the new order placing window. For FIFO accounts, stop levels will be automatically set in accordance with the stop levels of existing open positions for the same instrument. This procedure is required to comply with the FIFO rule.
   

1. Mathematical functions can now be applied to matrices and vectors.
   
   We continue expanding algorithmic trading and machine learning capabilities in the MetaTrader 5 platform. Previously, we have added new data types: matrices and vectors, which eliminate the need to use arrays for data processing. More than 70 methods have been added to MQL5 for operations with these data types. The new methods enable linear algebra and statistics calculations in a single operation. Multiplication, transformation and systems of equations can be implemented easily, without extra coding. The latest update includes mathematical functions.
   
   Mathematical functions were originally designed to perform relevant operations on scalar values. From this build and onward, most of the functions can be applied to matrices and vectors. These include MathAbs, MathArccos, MathArcsin, MathArctan, MathCeil, MathCos, MathExp, MathFloor, MathLog, MathLog10, MathMod, MathPow, MathRound, MathSin, MathSqrt, MathTan, MathExpm1, MathLog1p, MathArccosh, MathArcsinh, MathArctanh, MathCosh, MathSinh, and MathTanh. Such operations imply element-wise handling of matrices and vectors. Example:
   

   //---
     matrix a= {{1, 4}, {9, 16}};
     Print("matrix a=\n",a);
   
     a=MathSqrt(a);
     Print("MatrSqrt(a)=\n",a);
     /*
      matrix a=
      [[1,4]
       [9,16]]
      MatrSqrt(a)=
      [[1,2]
       [3,4]]
     */

   For MathMod and MathPow, the second element can be either a scalar or a matrix/vector of the appropriate size.
   
   The following example shows how to calculate the standard deviation by applying math functions to a vector.
   

   //+------------------------------------------------------------------+
   //| Script program start function                                    |
   //+------------------------------------------------------------------+
   void OnStart()
    {
   //--- Use the initializing function to populate the vector
     vector r(10, ArrayRandom); // Array of random numbers from 0 to 1
   //--- Calculate the average value
     double avr=r.Mean();       // Array mean value
     vector d=r-avr;            // Calculate an array of deviations from the mean
     Print("avr(r)=", avr);
     Print("r=", r);
     Print("d=", d);
     vector s2=MathPow(d, 2);   // Array of squared deviations
     double sum=s2.Sum();       // Sum of squared deviations
   //--- Calculate standard deviation in two ways
     double std=MathSqrt(sum/r.Size());
     Print(" std(r)=", std);
     Print("r.Std()=", r.Std());    
    }
   /*
     avr(r)=0.5300302133243813
     r=[0.8346201971495713,0.8031556138798182,0.6696676534318063,0.05386516922513505,0.5491195410016175,0.8224433118686484,...
     d=[0.30458998382519,0.2731254005554369,0.1396374401074251,-0.4761650440992462,0.01908932767723626,0.2924130985442671, ...
      std(r)=0.2838269732183663
     r.Std()=0.2838269732183663
   */ 
   //+------------------------------------------------------------------+
   //| Fills the vector with random values                              |
   //+------------------------------------------------------------------+
   void ArrayRandom(vector& v)
    {
     for(ulong i=0; i<v.Size(); i++)
       v[i]=double(MathRand())/32767.;
    }
   



2. Added support in template functions for notations matrix<double>, matrix<float>, vector<double>, vector<float> instead of the corresponding matrix, matrixf, vector and vectorf types.
   

3. Improved mathematical functions for operations with the float type. The newly implemented possibility to apply mathematical functions to 'float' matrix and vectors has enabled an improvement in mathematical functions applied to 'float' scalars. Previously, these function parameters were unconditionally cast to the 'double' type, then the corresponding implementation of the mathematical function was called, and the result was cast back to the 'float' type. Now the operations are implemented without extra type casting.
   
   The following example shows the difference in the mathematical sine calculations:
   

   //+------------------------------------------------------------------+
   //| Script program start function                                    |
   //+------------------------------------------------------------------+
   void OnStart()
    {
   //---  Array of random numbers from 0 to 1
     vector d(10, ArrayRandom);
     for(ulong i=0; i<d.Size(); i++)
      {
       double delta=MathSin(d[i])-MathSin((float)d[i]);
       Print(i,". delta=",delta);
      }
    }
   /*
      0. delta=5.198186103783087e-09
      1. delta=8.927621308885136e-09
      2. delta=2.131878673594656e-09
      3. delta=1.0228555918923021e-09
      4. delta=2.0585739779477308e-09
      5. delta=-4.199390279957527e-09
      6. delta=-1.3221741035351897e-08
      7. delta=-1.742922250969059e-09
      8. delta=-8.770715820283215e-10
      9. delta=-1.2543186267421902e-08
   */
   //+------------------------------------------------------------------+
   //| Fills the vector with random values                              |
   //+------------------------------------------------------------------+
   void ArrayRandom(vector& v)
    {
     for(ulong i=0; i<v.Size(); i++)
       v[i]=double(MathRand())/32767.;
    }

   
   
4. Added Activation and Derivative methods for matrices and vectors:
   

   AF_ELU	Exponential Linear Unit
   AF_EXP	Exponential
   AF_GELU	Gaussian Error Linear Unit
   AF_HARD_SIGMOID	Hard Sigmoid
   AF_LINEAR	Linear
   AF_LRELU	Leaky REctified Linear Unit
   AF_RELU	REctified Linear Unit
   AF_SELU	Scaled Exponential Linear Unit
   AF_SIGMOID	Sigmoid
   AF_SOFTMAX	Softmax
   AF_SOFTPLUS	Softplus
   AF_SOFTSIGN	Softsign
   AF_SWISH	Swish
   AF_TANH	Hyperbolic Tangent
   AF_TRELU	Thresholded REctified Linear Unit

   The neural network activation function determines how the weighted input signal sum is converted into a node output signal at the network level. The selection of the activation function has a big impact on the neural network performance. Different parts of the model can use different activation functions. In addition to all known functions, MQL5 also offers derivatives. Derivative functions enable fast calculation of adjustments based on the error received in learning.
   
   
5. Added Loss function for matrices and vectors. It has the following parameters:
   

   LOSS_MSE	Mean Squared Error
   LOSS_MAE	Mean Absolute Error
   LOSS_CCE	Categorical Crossentropy
   LOSS_BCE	Binary Crossentropy
   LOSS_MAPE	Mean Absolute Percentage Error
   LOSS_MSLE	Mean Squared Logarithmic Error
   LOSS_KLD	Kullback-Leibler Divergence
   LOSS_COSINE	Cosine similarity/proximity
   LOSS_POISSON	Poisson
   LOSS_HINGE	Hinge
   LOSS_SQ_HINGE	Squared Hinge
   LOSS_CAT_HINGE	Categorical Hinge
   LOSS_LOG_COSH	Logarithm of the Hyperbolic Cosine
   LOSS_HUBER	Huber

   The loss function evaluates the quality of model predictions. The model construction targets the minimization of the function value at each stage. The approach depends on the specific dataset. Also, the loss function can depend on weight and offset. The loss function is one-dimensional and is not a vector since it provides a general evaluation of the neural network.
   


6. Added matrix::CompareByDigits and vector::CompareByDigits methods for matrices and vectors. They compare the elements of two matrices/vectors up to significant digits.
   
   
7. Added support for MathMin and MathMax functions for strings. The functions will use lexicographic comparison: letters are compared alphabetically, case sensitive.
   
   
8. The maximum number of OpenCL objects has been increased from 256 to 65536. OpenCL object handles are created in an MQL5 program using the CLContextCreate, CLBufferCreate and CLProgramCreate functions. The previous limit of 256 handles was not enough for the efficient use of machine learning methods.
   
   
9. Added ability to use OpenCL on graphical card without 'double' support. Previously, only GPUs supporting double were allowed in MQL5 programs, although many tasks allow calculations using float. The float type is initially considered native for parallel computing, as it takes up less space. Therefore, the old requirement has been lifted.
   
   To set the mandatory use of GPUs with double support for specific tasks, use the CL_USE_GPU_DOUBLE_ONLY in the CLContextCreate call.
   

      int cl_ctx;
   //--- Initializing the OpenCL context
      if((cl_ctx=CLContextCreate(CL_USE_GPU_DOUBLE_ONLY))==INVALID_HANDLE)
        {
         Print("OpenCL not found");
         return;
        }

   
   
10. Fixed operation of the CustomBookAdd function. Previously, a non-zero value in the MqlBookInfo::volume_real field prevented the function from creating a Market Depth snapshot. The check is now performed as follows:
    
    The transmitted data is validated: type, price and volume data must be specified for each element. Also, MqlBookInfo.volume and MqlBookInfo.volume_real must not be zero or negative. If both volumes are negative, this will be considered an error. You can specify any of the volume types or both of them, while the system will use the one that is indicated or is positive:
    
       volume=-1 && volume_real=2 — volume_real=2 will be used,
    
       volume=3 && volume_real=0 — volume=3 will be used.
    
    Increased-precision volume MqlBookInfo.volume_real has a higher priority than MqlBookInfo.volume. Therefore, if both values are specified and are valid, volume_real will be used.
    
    If any of the Market Depth elements is described incorrectly, the system will discard the transferred state completely.
    
    
    
11. Fixed operation of the CalendarValueLast function. Due to an error, successive function calls after changes in the Economic Calendar (the 'change' parameter was set a new value after the call) could skip some events when using the currency filter.
    

    CalendarValueLast(change, result, "", "EUR")

12. Fixed ArrayBSearch function behavior. If multiple identical elements are found, a link to the first result will be returned, rather than a random one.
13. Fixed checks for template function visibility within a class. Due to an error, class template functions declared as private/protected appeared to be public.
    

1. Fixed errors and ambiguous behavior of MetaAssist.
2. Added support for the %terminal% macros which indicates the path to the terminal installation directory. For example, %terminal%\MQL5\Experts. 
   

   
   
   

3. Improved display of arrays in the debugger.
4. Increased buffer for copying values from the debugger.
   
5. Improved error hints.
6. Added indication of relative paths in the *.mproj project file. Previously, absolute paths were used, which resulted in compilation errors in case the project was moved.
   
7. Added automatic embedding of BMP resources as globally available 32-bit bitmap arrays in projects. This eliminates the need to call ResourceReadImage inside the code to read the graphical resource.
   

   'levels.bmp' as 'uint levels[18990]'
   

8. Improved reading of extended BMP file formats.
   
9. Updated UI translations.
10. Fixed errors reported in crash logs.