MetaTrader 5 Build 4730: Erweiterte Unterstützung von OpenBLAS und eine allgemeine Leistungsoptimierung

Terminal

1. Geänderte Berechnungen für die Werte von Positionen, Aufträge und Deals. Der Wert wird nun in der Kontowährung und nicht mehr in der Basiswährung des Handelssymbols angezeigt:

   

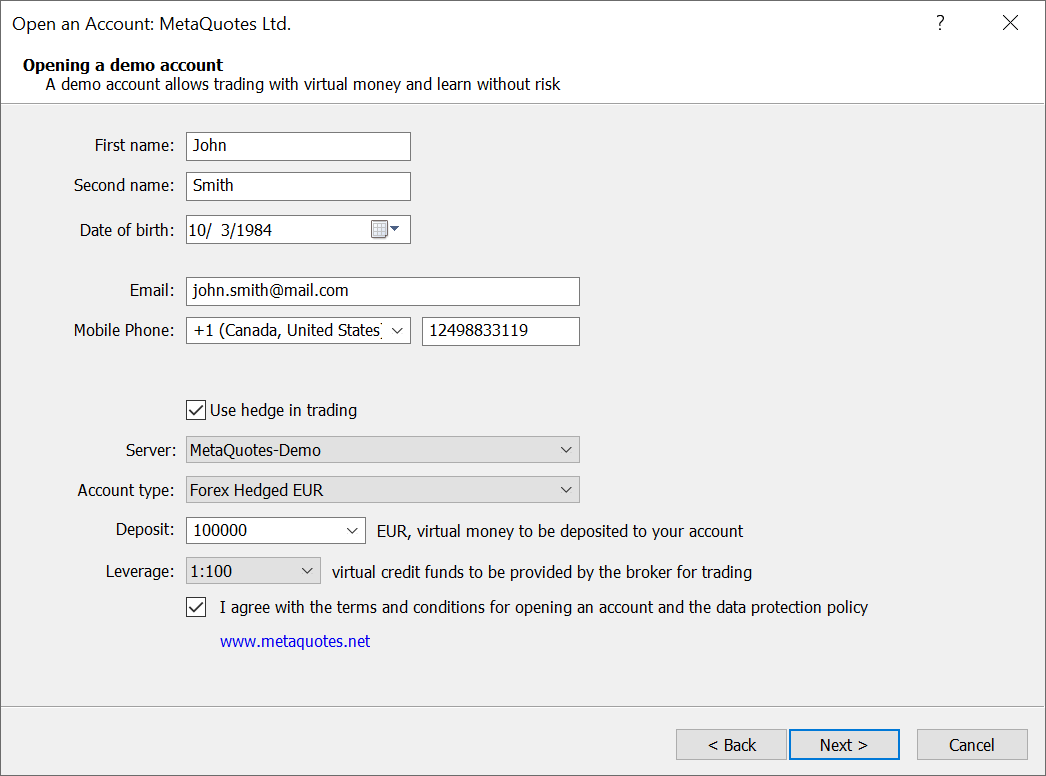
2. Das Feld zur Eingabe des Geburtsdatums bei der Eröffnung von Demokonten hinzugefügt.

   
   

   
   
3. Die Skalierung der Indikatoren, die im Unterfenster des Charts angezeigt werden, wurde korrigiert. Bei einigen Oszillatoren konnten bisher die minimalen und maximalen Skalenwerte falsch gewählt werden.
4. Optimiertes und beschleunigtes Entpacken von Tickdaten und Kursverläufen, was die Ladegeschwindigkeit des Charts erhöht.
5. Die Bearbeitung der Textfarbe im E-Mail-Erstellungsfenster wurde korrigiert.
6. Aktualisierte Übersetzungen der Nutzeroberfläche.

1. Es wurden neue Methoden von OpenBLAS hinzugefügt:
   
   
   • EigenSolver2 – Berechnung von verallgemeinerten Eigenwerten und Eigenvektoren für ein Paar gewöhnlicher, quadratischer Matrizen (Lapack-Funktion GGEV).
   • EigenSolverX – berechnet Eigenwerte und Eigenvektoren einer regulären quadratischen Matrix im Expertenmodus, d.h. mit der Möglichkeit, den Berechnungsalgorithmus zu beeinflussen, und der Möglichkeit, begleitende Berechnungsdaten zu erhalten (Lapack-Funktion GEEVX).
   • EigenSolver2X – berechnet Eigenwerte und Eigenvektoren für ein Paar regulärer quadratischer Matrizen im Expertenmodus, d.h. mit der Möglichkeit, den Berechnungsalgorithmus zu beeinflussen, und der Möglichkeit, begleitende Berechnungsdaten zu erhalten (Lapack-Funktion GGEVX).
   • EigenSolverShur – Berechnung von Eigenwerten, der oberen Dreiecksmatrix in Schur-Form und der Matrix der Schur-Vektoren (Lapack-Funktion GEES).
   • EigenSolver2Shur – Berechnung von Eigenwerten, verallgemeinerten Eigenvektoren, verallgemeinerten Schur-Formen sowie linken und rechten Schur-Vektoren für ein Paar regulärer quadratischer Matrizen (Lapack-Funktion GGES).
   • EigenSolver2Blocked – Berechnung von verallgemeinerten Eigenwerten und Eigenvektoren für ein Paar regulärer quadratischer Matrizen unter Verwendung eines Blockalgorithmus (Lapack-Funktion GGEV3).
   • EigenSolver2ShurBlocked – berechnet für ein Paar regulärer quadratischer Matrizen Eigenwerte, verallgemeinerte Eigenvektoren, verallgemeinerte Schur-Formen sowie linke und rechte Schur-Vektoren unter Verwendung eines Blockalgorithmus (Lapack-Funktion GGES3).
   • EigenSymmetricRobust – Berechnung von Eigenwerten und Eigenvektoren einer symmetrischen oder hermiteschen (komplex konjugierten) Matrix unter Verwendung des MRRR-Algorithmus (Multiple Relatively Robust Representations, MRRR) (Lapack-Funktionen SYEVR, HEEVR).
   • EigenSymmetricBisect – Berechnung von Eigenwerten und Eigenvektoren einer symmetrischen oder hermiteschen (komplex konjugierten) Matrix unter Verwendung des Bisektionsalgorithmus (Lapack-Funktionen SYEVX, HEEVX).
   
   
2. Es wurden neue Methoden für komplexe Matrizen hinzugefügt:
   
   
   • TransposeConjugate – erstellt eine konjugiert-transponierte Matrix.
     

     matrix<complex<T>> matrix<complex<T>>::TransposeConjugate(void) const;

     Die Methode gibt eine neue konjugiert-transponierte Matrix zurück, in der die Elemente der ursprünglichen Matrix transponiert und in ihre komplexen Konjugierten umgewandelt werden.
     
     Wenn ein Fehler auftritt, wird eine leere Matrix zurückgegeben. Verwenden Sie die Funktion GetLastError, um den Fehlercode zu ermitteln.
     
     
   • CompareEqual – absoluter Vergleich von zwei Matrizen.
     

     int matrix<T>::CompareEqual(const matrix<T>& mat) const

     Die Rückgabewerte sind:
     
     
     • -1 – wenn das Element der Matrix A kleiner ist als das entsprechende Element der Matrix B.
     • 0 – wenn alle Elemente der Matrizen A und B identisch sind.
     • 1 – wenn das Element der Matrix A größer ist als das entsprechende Element der Matrix B.
     
     Die Methode kann auch Fehler zurückgeben, wenn die Eingabedaten ungültig sind. Um den Fehlercode zu erhalten, verwenden Sie die Funktion GetLastError.
     
   
   
3. Es wurde die Python-Unterstützung bis zur Version 3.13 für das entsprechende Integrationspaket hinzugefügt. Um das Paket zu aktualisieren, führen Sie den folgenden Befehl aus:
   

   pip install --upgrade MetaTrader5

4. Das Überspringen des ersten Timer-Ereignisses wurde behoben. Ein Fehler trat auf, wenn ein Timer innerhalb des OnTimer-Handlers gestartet wurde.

• Die Berechnung von Werten für Eingabevariablen im Debugger-Modus wurde korrigiert. In einigen Fällen wurde anstelle des Wertes die Meldung „unbekannter Bezeichner“ (unknown identifier) angezeigt.

• Die Suche nach den erforderlichen Kreuzkursen für die Währungsumrechnung beim Testen von Anwendungen mit Deviseninstrumenten wurde korrigiert.
  
  

Web-Terminal

1. Unterstützung für die Ausführungsart Request für großvolumige Aufträge wurde hinzugefügt.
2. Es wurde die Unterstützung für eine erweiterte Beschreibung der Ursache für von einem Makler abgelehnte Anfragen hinzugefügt.
3. Korrigiert wurde das Formular zur Eröffnung eines Kontos. Es werden nun die Informationen entsprechend den Maklereinstellungen angefordert.
4. Die Ländererkennung bei der Registrierung von Demokonten wurde korrigiert.
5. Die Ausrichtung des Dialogs, der die Warnung zum Ein-Klick-Handel anzeigt, wurde korrigiert.